Hypotézy:

• Prierezy po deformácii zostanú rovinné, rovnobežné a vzdialenosť sa medzi prierezmi nemení.
• Os prúta nezostane priama, ale sa medzi uvažovanými prierezmi pootočí o uhol γ_xz.
• Prierezy nezostanú kolmé na os prúta a vzájomne sa posunú vo svojich rovinách ako tuhé celky.

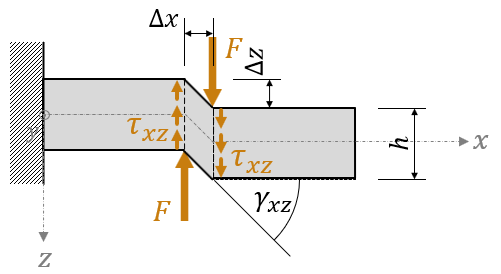
Z hypotézy o pretvorení vyplýva, že pôvodné rovnobežky s osou x sa skosia o uhol Τ_xz (skos nastáva v rovine xz):

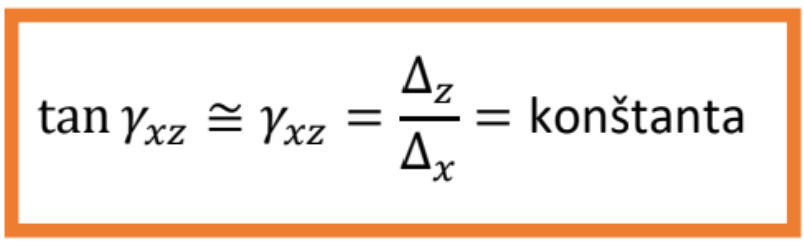
V lineárnej oblasti platí Hookov zákon pre šmyk, obdobne ako pre osový ťah, resp. tlak:

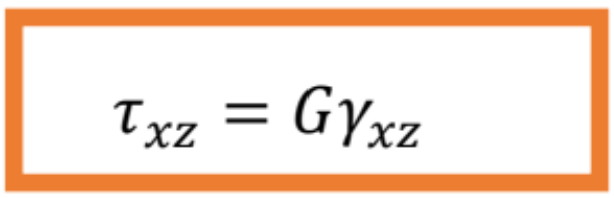
kde G je modul pružnosti v šmyku [Pa, N/m2| a  je Poissonovo číslo.

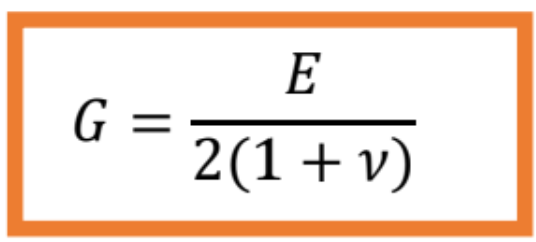
Bližšie odvodenie tejto materiálovej konštanty je v časti 4.

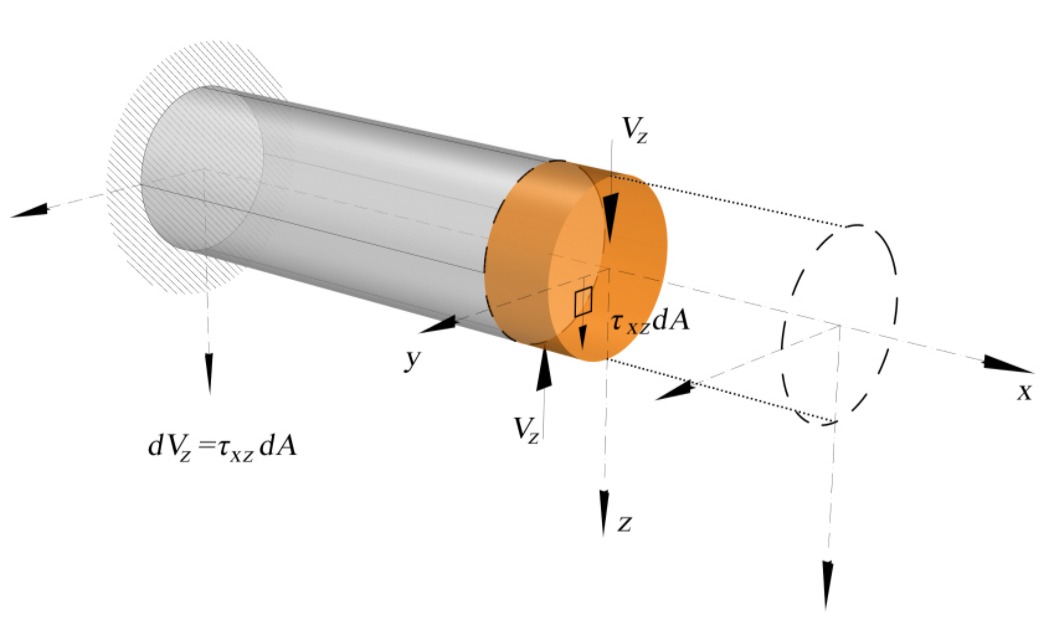
Z hypotézy o rovinnosti prierezov pred a po deformácii a zachovaní ich vzdialenosti vyplýva, že v bodoch prierezu vzniká iba tangenciálne napätie, ktoré má na základe Hookovho zákona konštantnú hodnotu vo všetkých bodoch. Indexy šmykového napätia udávajú v ktorej rovine vniká jednoduchý šmyk.

Rozloženie a veľkosť elementárnych síl dV_z musí byť staticky ekvivalentné prečnej sile V_z. Pre teleso máme 6 podmienok rovnováhy. 4 podmienky sú splnené identicky na základe statickej ekvivalencie elementárnych síl dV_z  a výslednej priečnej sily V_z.

1. ∑F_x=0      
2. ∑F_y=0      
3. ∑M_y=0      
4. ∑M_z=0  
5. Piata vedie na určenie tangenciálneho napätia

Veľkosť šmykového napätia v ľubovoľnom bode prierezu namáhaného priečnou silou v rovine xz určíme podľa vzťahu

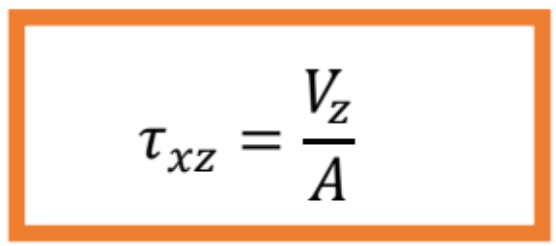
6. Šiesta potvrdzuje, že priečna sila prechádza ťažiskom

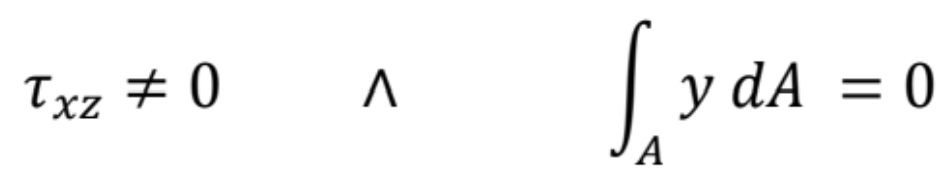
Statický moment prierezovej plochy A k osi z je nulový vtedy, ak os z je ťažisková os. Tým je potvrdené, že priečna sila V_z prechádza ťažiskom prierezu.

Podporené grantom: KEGA 030STU-4/2023 

Vedúca projektu: Doc. Tvrdá

Zdroj: Dický, J., Mistríková, Z., Sumec, J.: Pružnosť a plasticita I. Vydavateľstvo STU. 2005.