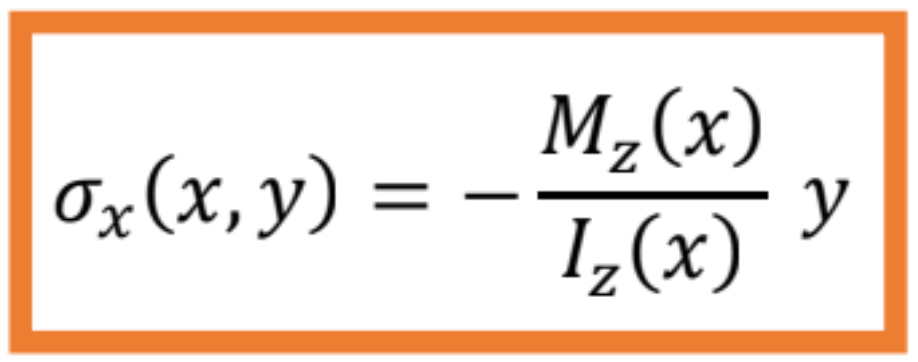Vyššie uvedené hypotézy si objasníme na elemente nosníka dĺžky dx namáhaného na oboch koncoch kladnými ohybovými momentmi My pôsobiacimi v rovine symetrie jeho priečneho rezu.
Element bez zaťaženia:
- Krajné prierezy sú rovinné a rovnobežné.
- Vlákna majú rovnakú dĺžku po celej výške prierezu.
Element po zaťažení:
- Krajné prierezy sa pootočili o uhol dφ.
- Dĺžka vlákien dx, v rovine xy, medzi bodmi
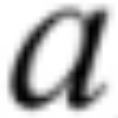a b sa nezmení. - Vlákna nad touto rovinou sa skrátia.
- Vlákna pod touto rovinou sa predĺžia.
- Zmena dĺžky vlákien je úmerná zvislej vzdialenosti od roviny xy.
V dôsledku experimentálnych meraní sa zistilo, že:
- Pred zaťažením lákna prierezu dx sú rovnobežné s osou y.
- Po zaťažení sa zmenia na sústredné krivky.
- Prierezy ostanú rovinné a kolmé na vlákna.
- V dôsledku toho sa predpokladá, že napätia
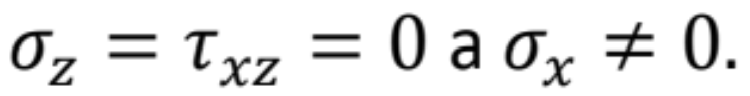
Z hore uvedeného obrázku si vieme vyjadriť:
- dĺžku osi nosníka ako dĺžku oblúka: 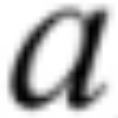b=p.dφ
- dĺžku vlákna vo vzdialenosti z od osi nosníka ako: cd=(p+z).dφ
Pôvodná dĺžka vlákien bola rovnaká z čoho vyplýva, že absolútnu a relatívnu zmenu dĺžky vlákna cd vyjadríme takto:
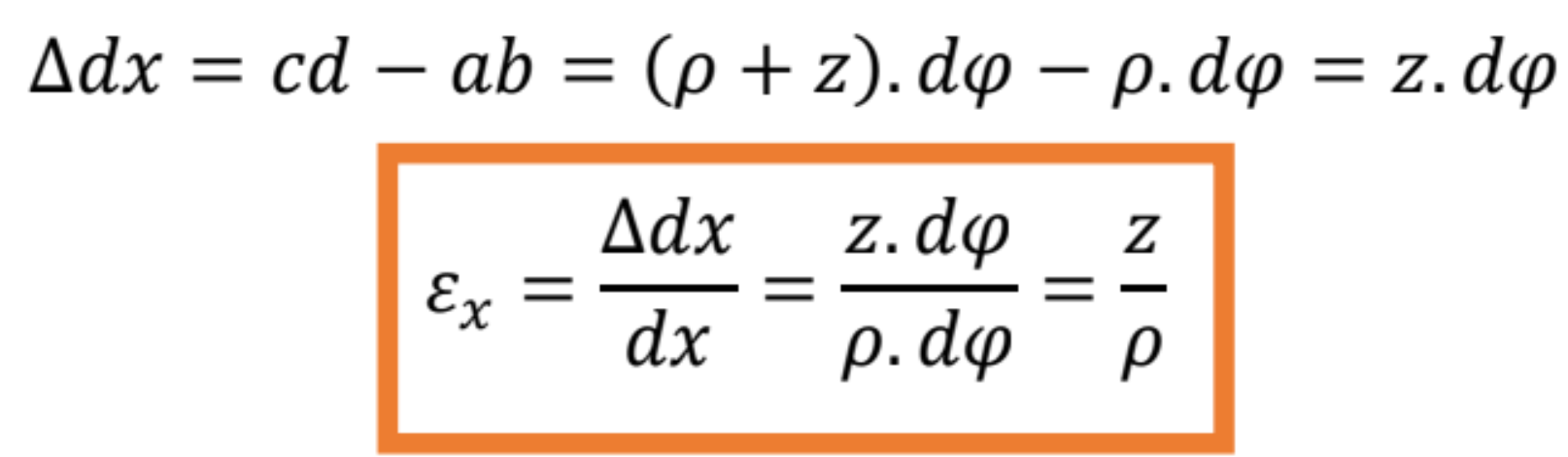
Pomerná zmena dĺžky vlákna je priamo úmerná jeho vzdialenosti od osi prúta z a nepriamo úmerná polomeru krivosti zakrivenej osi prúta ρ.
Podľa Hookovho zákona pre jednoduchý ťah spolu s predchádzajúcim vzťahom platí:
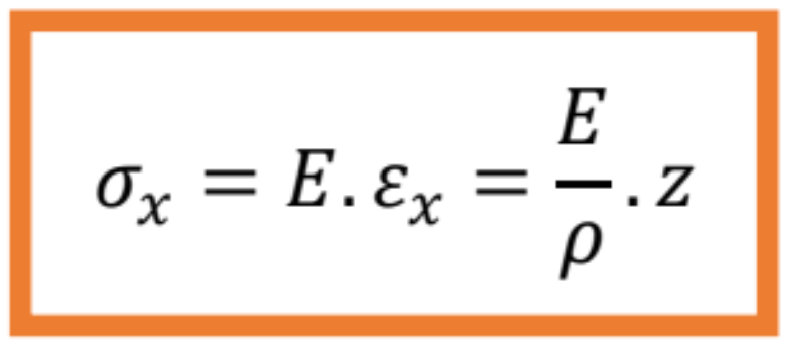
Z rovnice vyplýva:
- Normálové napätie sa mení lineárne po výške prierezu.
- Vlákna ležiace v rovine xy sú v dôsledku nulovej vzdialenosti z nulové, σx = 0.
- Rovinu xy nazývame neutrálnou rovinou nosníka a jej priesečnicu s rovinou prierezu neutrálnou osou prierezu.
Preskúmajme podmienky rovnováhy na nasledujúcom elemente, aby sme odvodili vzťah pre výpočet normálových napätí.
Z obrázku je zrejmé, že zo šiestich podmienok rovnováhy sú 3 splnené identicky.
Zo štvrtej podmienok vyplýva:
Dosadením napätia do predchádzajúceho výrazu a po úprave dostaneme
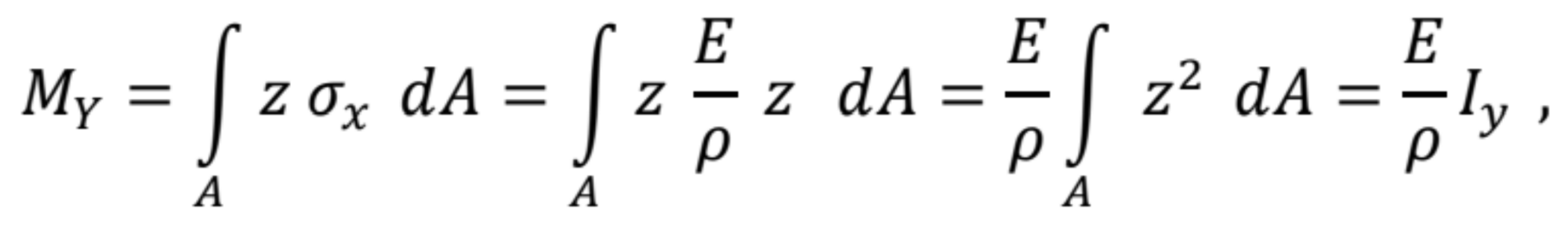
kde 
je moment zotrvačnosti prierezu k osi y.
Z rovnice pre výpočet napätí vyplýva, že
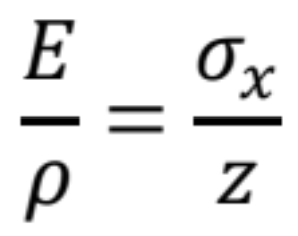
Dosadením tohto výrazu do rovnice pre výpočet My a úprave dostaneme vzťah pre výpočet normálového napätia, za predpokladu, že My a Iy sú konštantné.
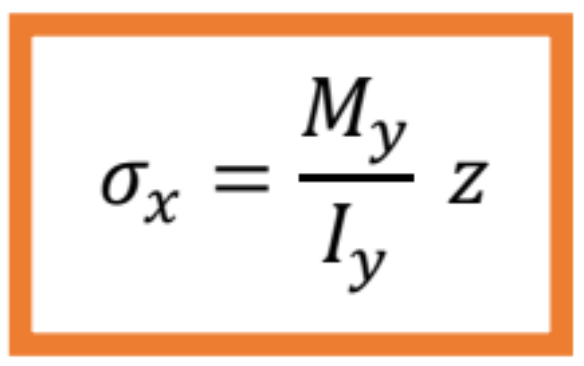
Ak sú však ohybový moment a moment zotrvačnosti prierezu funkcie, meniace sa po dĺžke osi prúta, t. j. My = My(x), resp. Iy = Iy(x), potom platí:
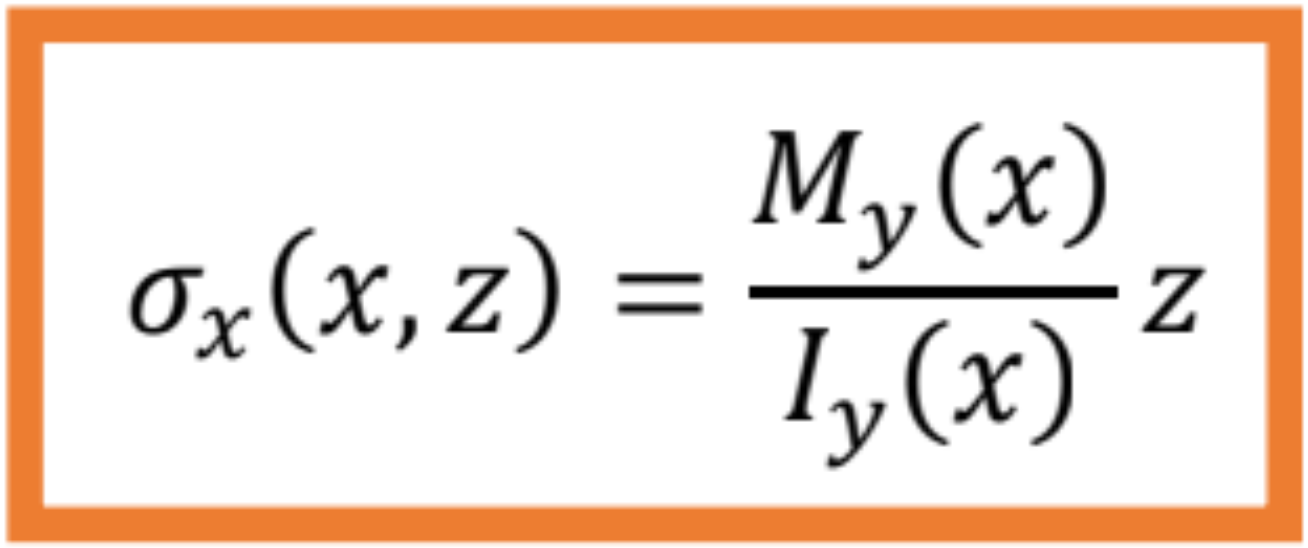
Poznámky:
- Napätie σx je funkciou súradníc (x,z) bodu nosníka, ale nezávisí od súradnice y bodu v priereze. Z výrazu vyplýva, že napätie vo všetkých bodoch prierezu, ktoré sú rovnako vzdialené od osi y, bude rovnaké.
- Predchádzajúca rovnica bola odvodená v prípade, že vektor kladného ohybového momentu My je orientovaný v smere kladnej osi y a vyvoláva v bodoch prierezu s kladnou súradnicou z kladné (ťahové) normálové napätie. Ak by bol podľa inej znamienkovej konvencie kladný ohybový moment My opačne orientovaný, musí byť vo vzťahu na výpočet napätí znamienko mínus, aby napätie v bodoch s kladnou súradnicou z bolo záporné.
Pretože žiadne vonkajšie horizontálne sily Fix na elemente nepôsobia, potom z piatej podmienky rovnováhy vyplýva:
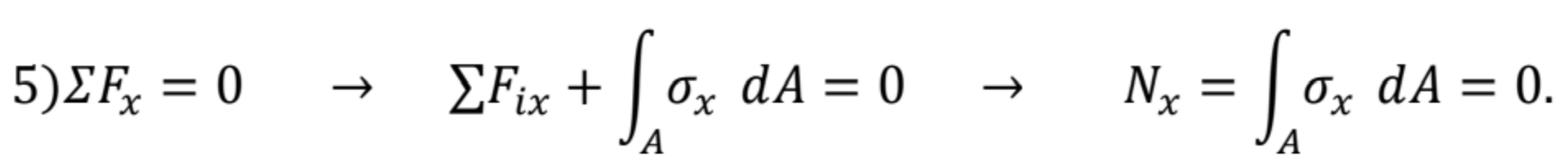
Dosadením 
do posledného výrazu po úprave dostaneme
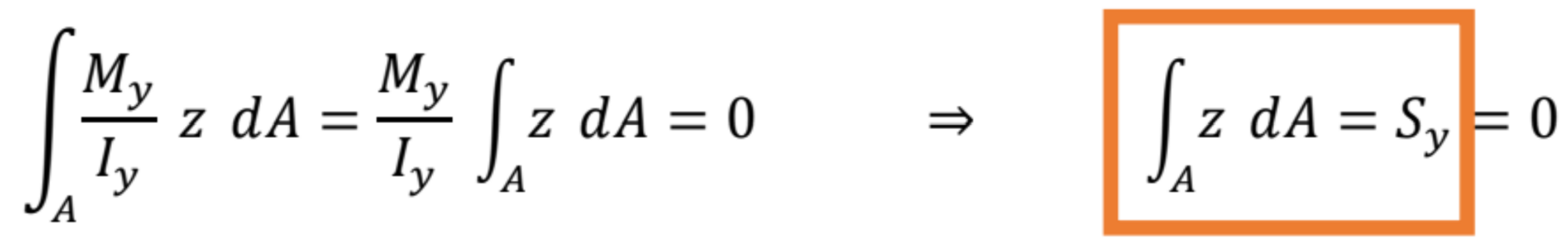
Statický moment k neutrálnej osi y, označený Sy, musí byť rovný nule, t. j. os y je potom ťažiskovou osou.
Z poslednej podmienky rovnováhy dostaneme:
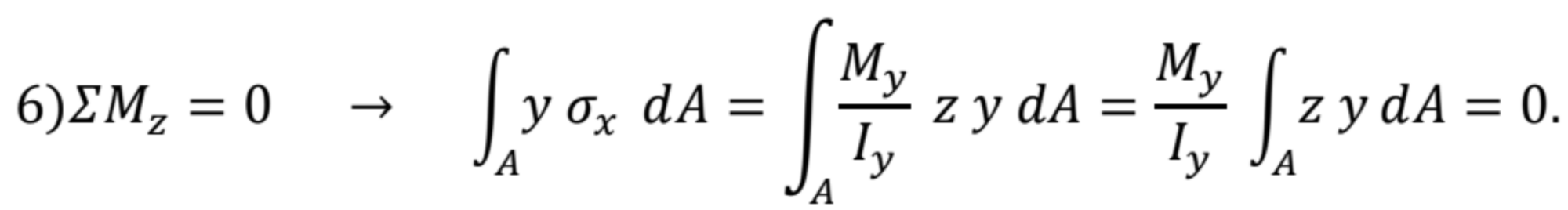
Vzťah je rovný nule za predpokladu, že deviačný moment 
je rovný nule. Potom osi y a z sú hlavné centrálne osi zotrvačnosti, pretože os y je ťažiskovou osou, čo vyplývalo zo statického momentu plochy.
Priebeh normálových napätí σx v priereze od ohybového momentu My je na nasledujúcom obrázku.
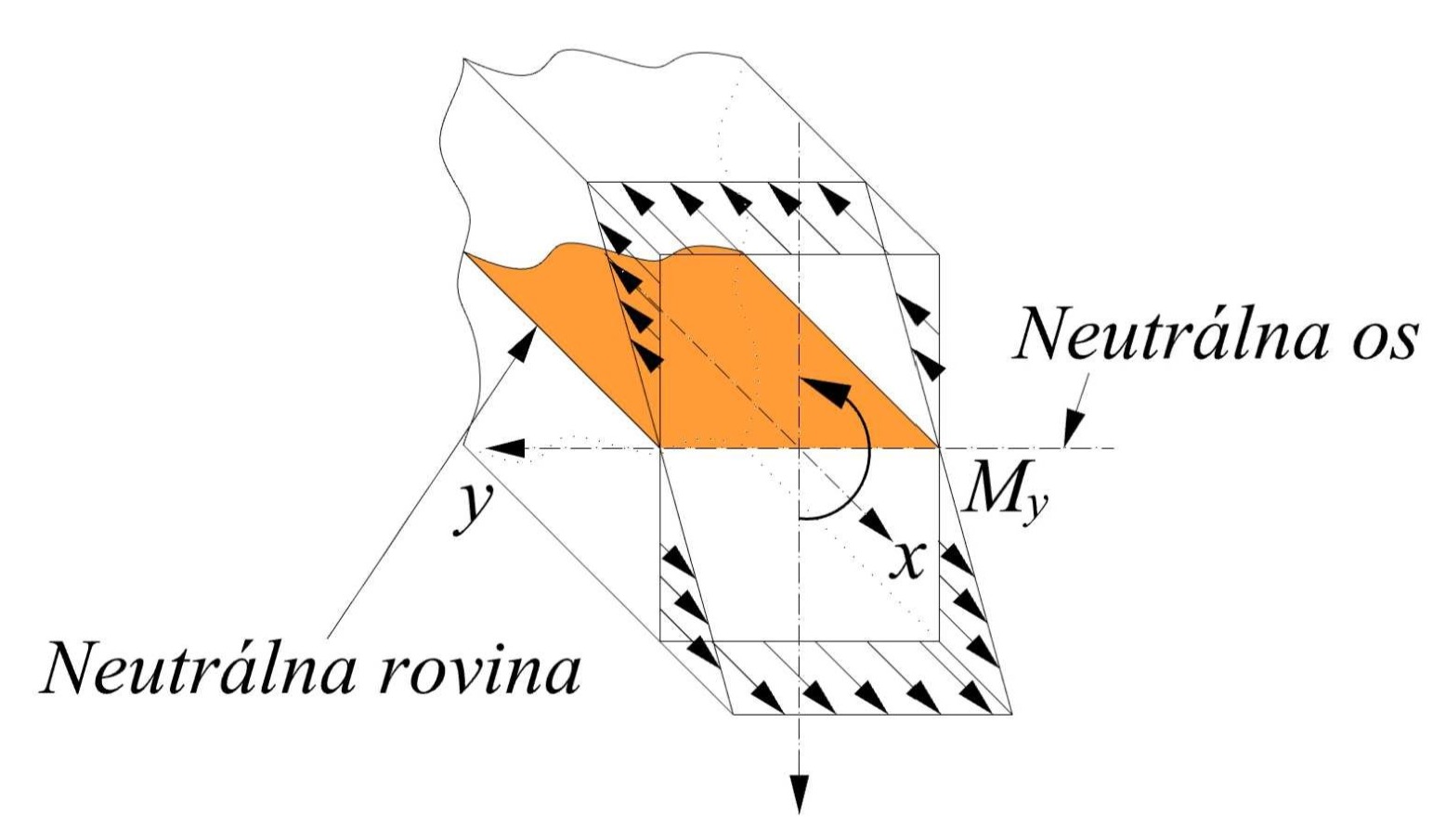
Tento spôsob namáhania nastáva nielen v prierezoch symetrického, ale aj všeobecného tvaru, ak
- rovina, v ktorej pôsobí ohybový moment, obsahuje jednu z centrálnych hlavných osí zotrvačnosti prierezu,
- je takto pôsobiaci moment jedinou silou pôsobiacou v priereze prúta, hovoríme o jednoduchom čistom ohybe.
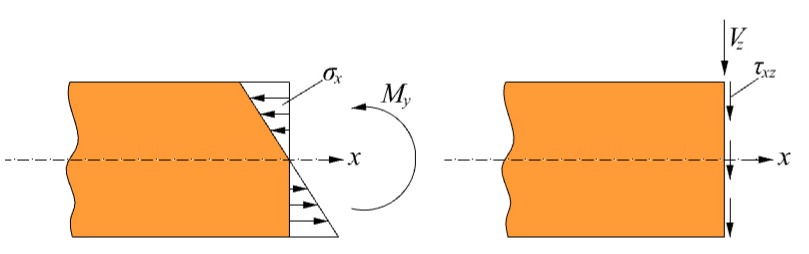
Ak na nosník pôsobí ľubovoľné priečne zaťaženie, ktorého rovina obsahuje jednu z centrálnych hlavných osí zotrvačnosti prierezu (napr. rovina xz), potom v priereze vzniká okrem ohybového momentu My aj priečna sila Vz. V takom prípade hovoríme o jednoduchom ohybe. Pri tomto spôsobe namáhania vznikajú v priereze okrem normálových napätí aj tangenciálne (šmykové) napätia v rovine prierezu τxz.
Normálové napätia na obrázku nemôžu byť v rovnováhe s priečnou silou, pretože smery ich pôsobenia v priereze sú na seba kolmé a rovnako účinok tangenciálnych napätí pôsobiacich v rovine prierezu nemôže byť v rovnováhe s ohybovým momentom.
Z toho vyplýva, že normálové napätia môžeme počítať podľa vzťahov odvodených pre čistý ohyb a tangenciálne napätia len od priečnej sily.
Priebehy napätí v priereze všeobecného tvaru v dôsledku kladných ohybových momentov My a Mz pôsobiacich v smeroch hlavných osí zotrvačnosti y, z sú uvedené na ďalšom obrázku.
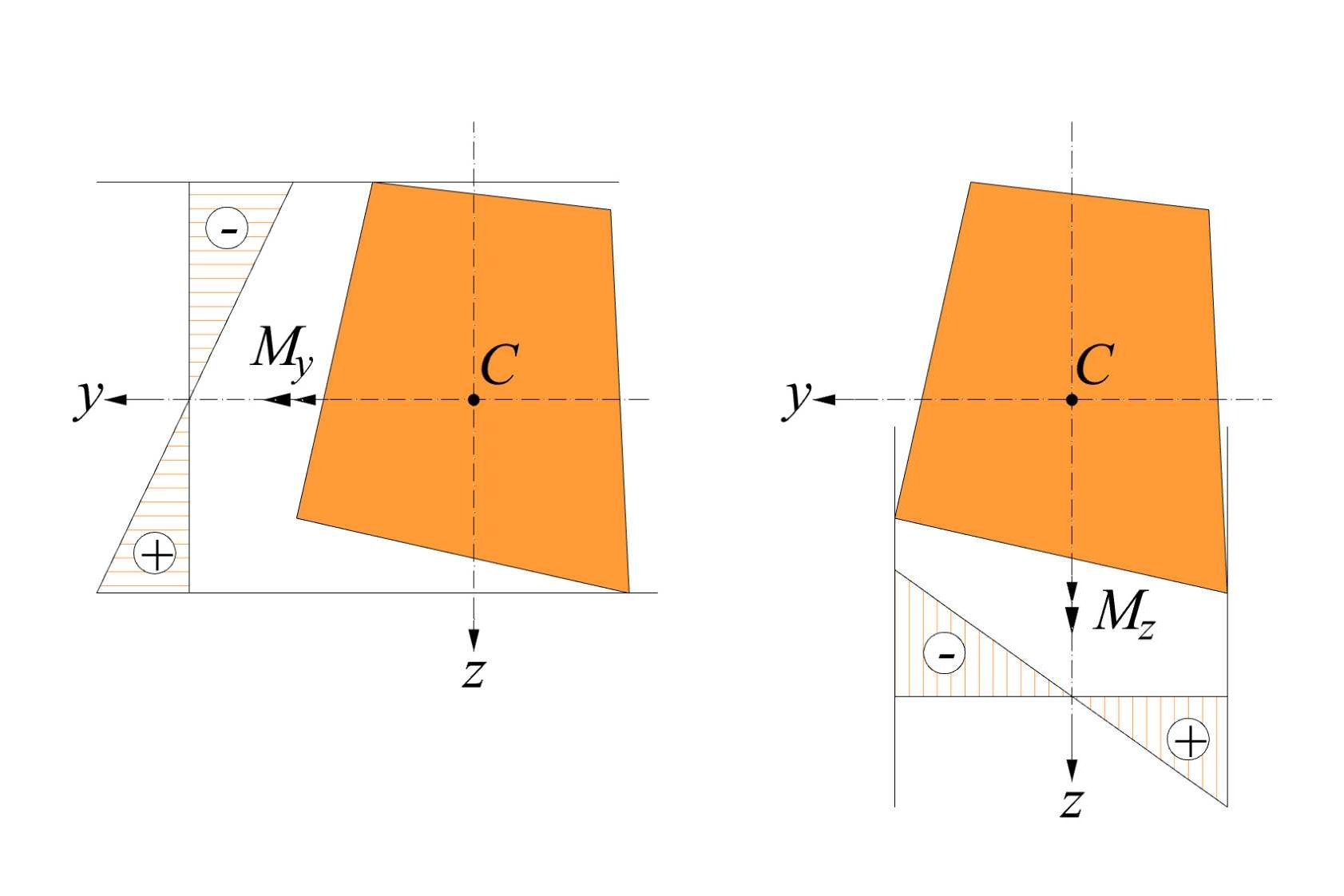
Kladný ohybový moment My vyvoláva v prvom kvadrante (+y,+z) ťahové napätie (+) a je vyjadrených vzťahom
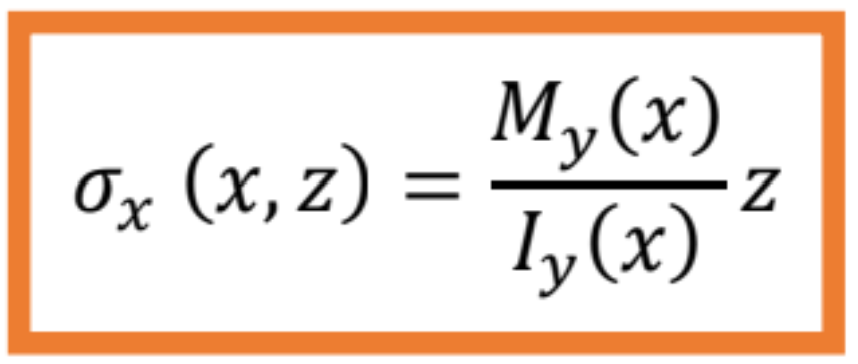
pričom kladný ohybový moment Mz vyvoláva v prvom kvadrante (+y,+z) tlakové napätie (-), potom
