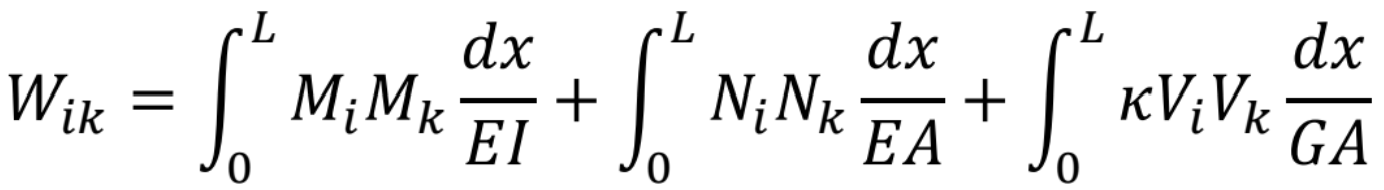Virtuálna práca – (myslená možná práca) je definovaná ako skalárny súčin vektora sily a vektora premiestnenia
![]()
pričom sila a premiestnenie vzájomne nesúvisia.
Rozlišujeme virtuálnu prácu:
- skutočná sila na virtuálnom premiestnení,
- virtuálna sila na skutočnom premiestnení.
Virtuálne premiestnenie – ľubovoľné premiestnenie v medziach vnútorných a vonkajších väzieb v lineárne pružnej oblasti.
Virtuálna práca vonkajších síl
Virtuálna práca – princíp vysvetlený na príklade.
- Skupina síl s indexom i pôsobí prostý nosník.
- Skupina síl s indexom k pôsobí na ten istý prostý nosník.
Virtuálna práca skupiny síl i na premiestneniach vyvolaných skupinou síl k je definovaná:
![]()
- Pričom sila Fi je násobená premiestnením (dráhou) Δik, ktoré je zapríčinené silami skupiny k, t. j. „sila a premiestnenie príčinne nesúvisia”.
- Δik, φik – prvý index udáva miesto, druhý index príčinu.
Vo všeobecnosti pre virtuálnu prácu Aik píšeme:
![]()
Virtuálna práca skupiny síl k na premiestneniach vyvolaných skupinou síl i je definovaná:
![]()
Vo všeobecnosti pre virtuálnu prácu Aki píšeme:
![]()
Virtuálna práca vnútorných síl
Nosník je zaťažený skupinou síl i. Vplyvom zaťaženia vzniknú prierezové sily:
- ohybový moment Mi,
- priečna sila Vi,
- osová sila Ni.
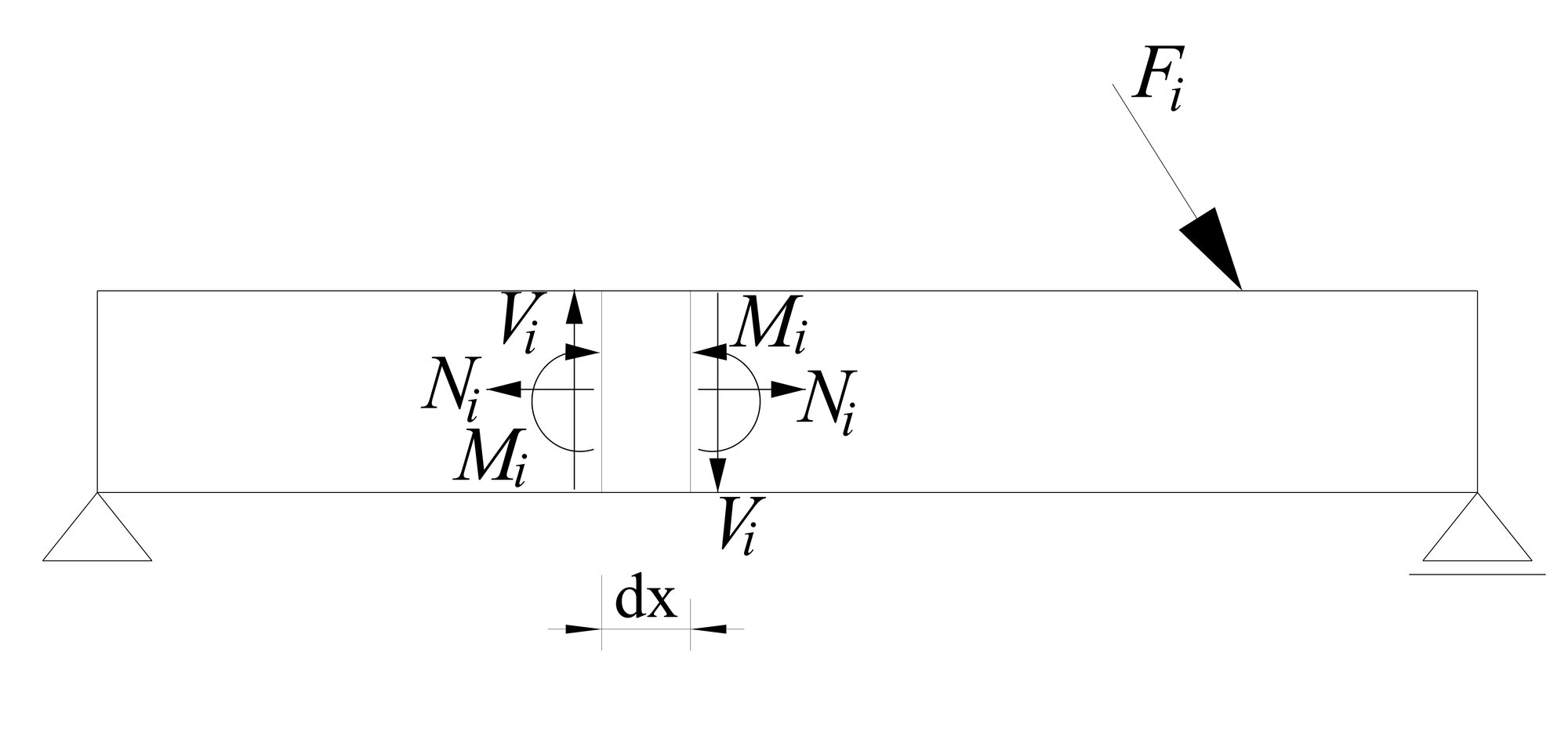
Element nosníka dx sa zdeformuje o:
- vzájomné pootočenie prierezov prvku od ohybového momentu Mi,
![]()
- vzájomné priečne posunutie (skos) prierezov prvku od priečnej sily Vi,
![]()
- vzájomné posunutie prierezov prvku v smere osi prúta od osovej sily Ni.
![]()
Ak je prostý nosník je zaťažený skupinou síl k, vzniknú vnútorné sily:
- ohybový moment Mk,
- priečna sila Vk,
- osová sila Nk.
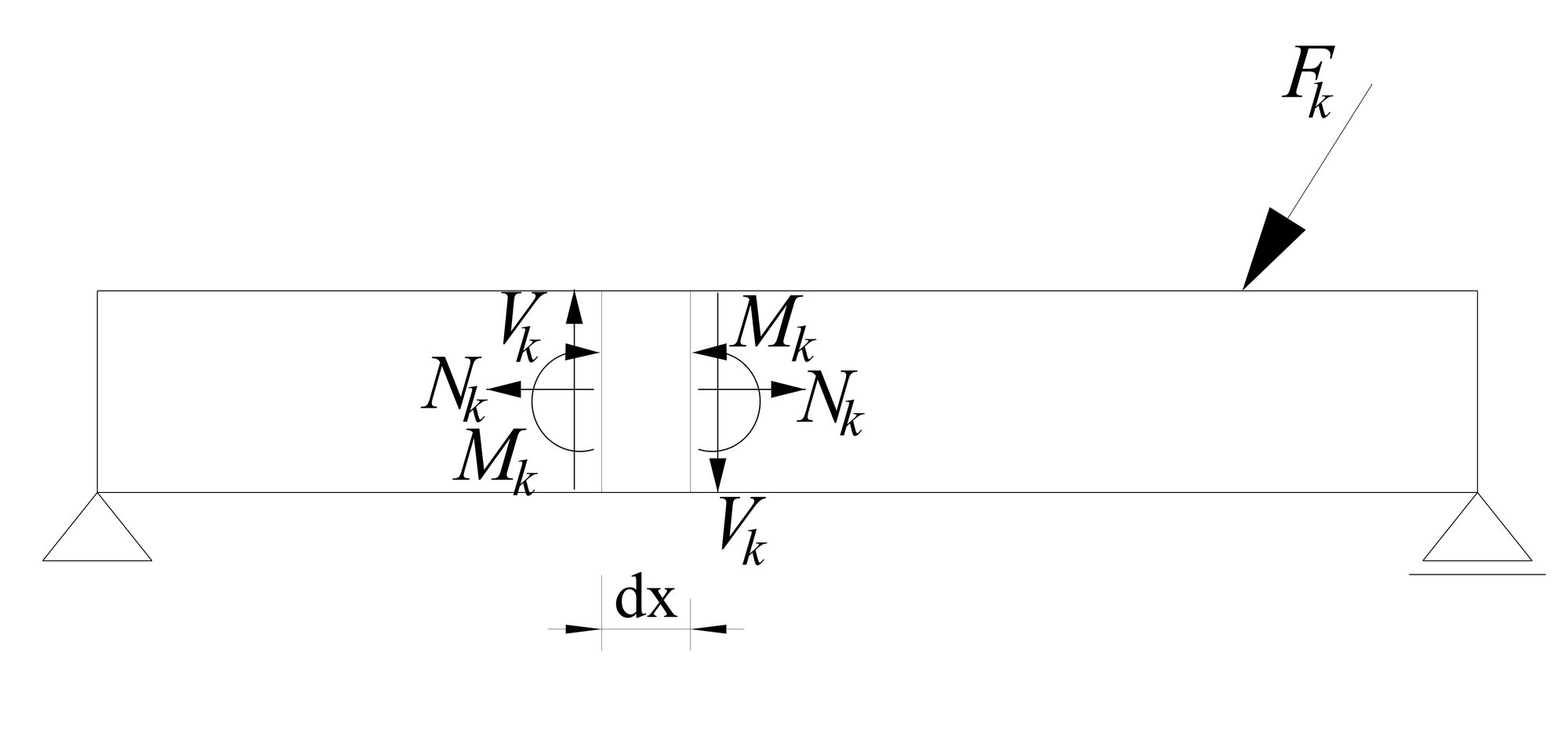
Element nosníka dx sa zdeformuje a analogicky môžeme písať hodnoty deformácií:
- vzájomné pootočenie prierezov prvku od ohybového momentu Mk,
![]()
- vzájomné priečne posunutie (skos) prierezov prvku od priečnej sily Vk,
![]()
- vzájomné posunutie prierezov prvku v smere osi prúta od osovej sily kN.
![]()
Virtuálna práca vnútorných síl je myslená práca vnútorných (prierezových) síl skupiny i (vzniknutých ako dôsledok vonkajšieho zaťaženia i) na deformáciách, ktoré sú zapríčinené skupinou síl k.
Na diferenciálnom elemente pôsobia prierezové sily skupiny i (Mi, Vi, Ni) a ten istý element je od síl skupiny k zdeformovaný (ΔkM, ΔkV, ΔkN). Virtuálna práca vnútorných (prierezových) síl na elemente je:
![]()
Ak za deformácie Δ dosadíme vyššie uvedené vzťahy a integrujeme po celej dĺžke nosníka „L“ dostaneme výraz:
![]()
Analogicky, sily skupiny k (Mk, Nk, Vk) vykonajú virtuálnu prácu na premiestneniach (ΔiM, ΔiV, ΔiN) vyvolanými skupinou síl i: