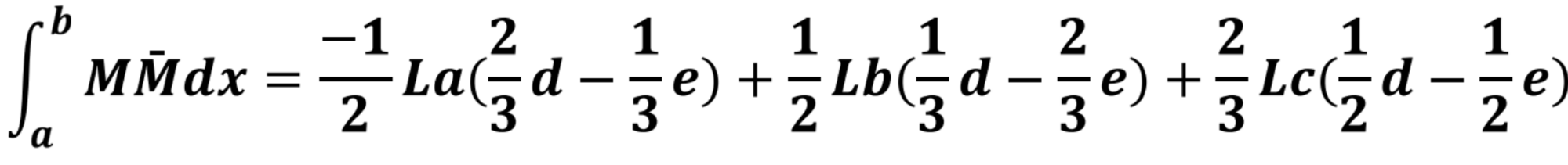Pri riešení premiestnení rámových konštrukcií vo väčšine prípadov zanedbávame
vplyv osových a priečnych síl. Z výrazu
na pravej strane ostane zväčša len vplyv ohybových momentov (ak neuvažujeme zaťaženie zmenou teploty).
Potom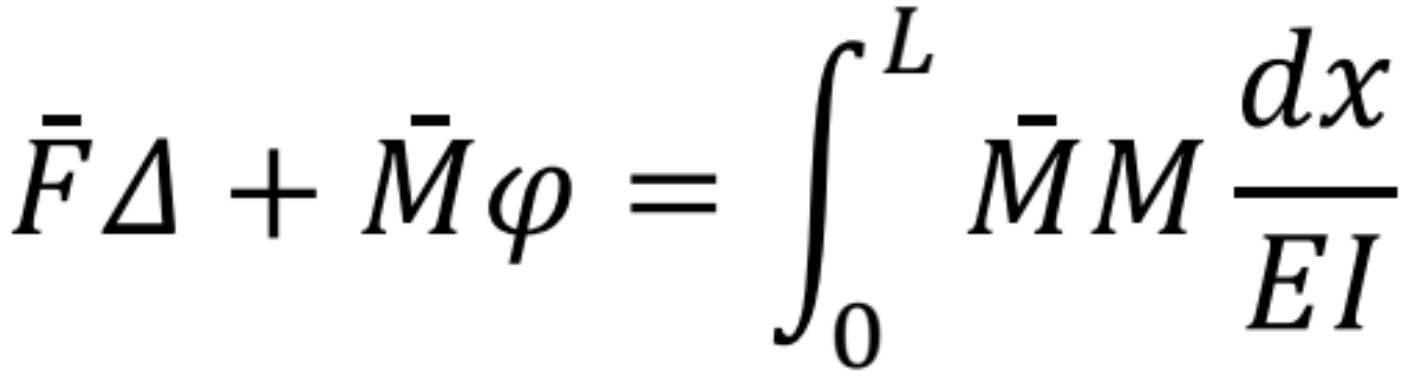 
Ak sú jednotlivé prúty priame s konštantnou ohybovou tuhosťou El na prúte, môžeme integrovanie rozdeliť na súčet integrálov v jednotlivých úsekoch (prútoch s rovnakou tuhosťou El).
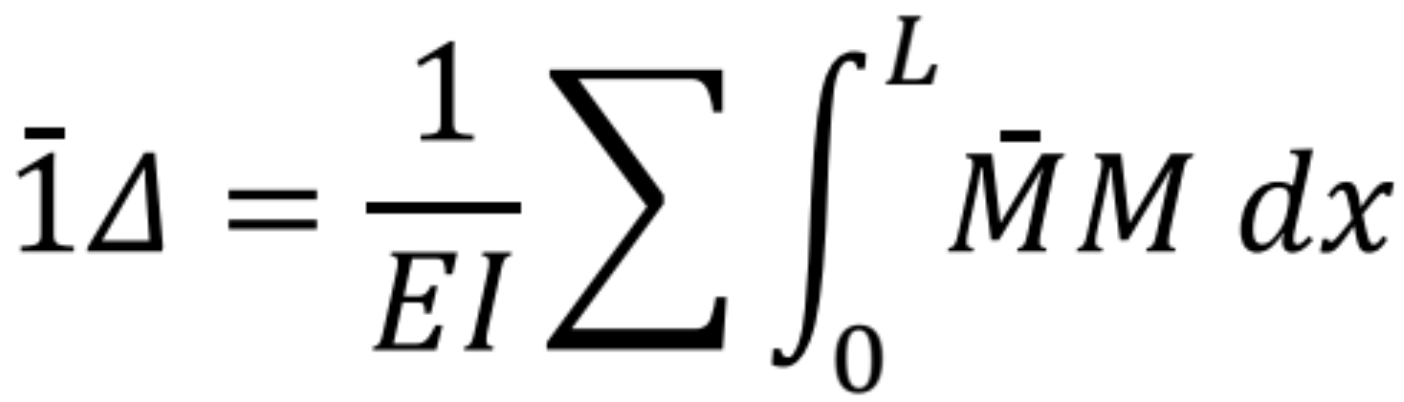
Vereščagino pravidlo – numerická integrácia
Hodnotu integrálu možno vyčísliť numerickou integráciou (Vereščaginovo pravidlo), ak:
- ak aspoň jeden z obrazcov M alebo
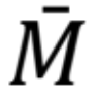je lineárnou funkciou (tvar obrazca: obdĺžnik, trojuholník, lichobežník), - druhý obrazec môže byť ľubovoľnou funkciou.
Potom:
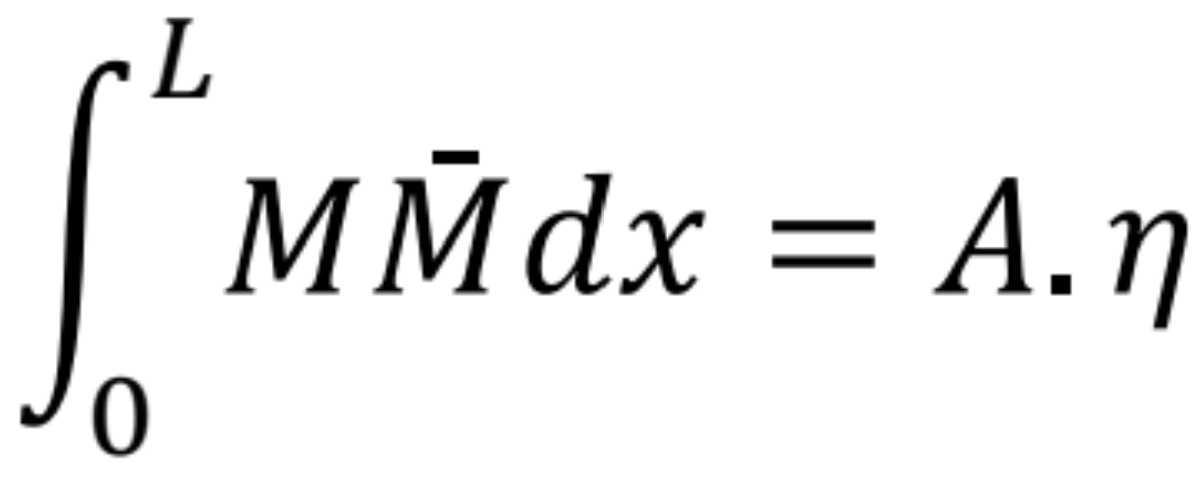
kde A je plocha momentového obrazca a η je poradnica pod ťažiskom plochy A na druhom momentovom obrázku.
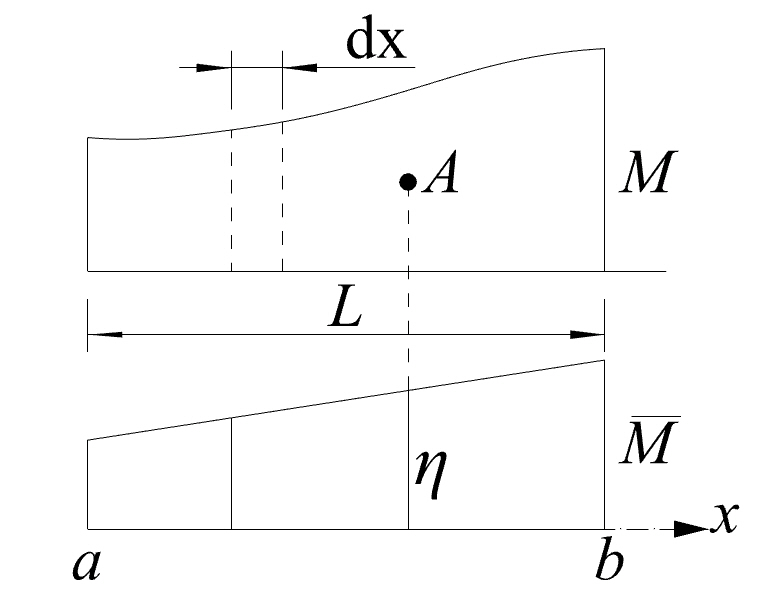
V tomto prípade momentové momenty M, môžeme nahradiť jednoduchými útvarmi, ktorých vieme vypočítať ťažisko a plochu. Ide o kombináciu dvoch trojuholníkov (alebo obdĺžnika, trojuholníka) a paraboly. Pri obrázkoch M ide o kombináciu dvoch trojuholníkov (alebo obdĺžnika, trojuholníka).
Príklad kombinácie 1 – parabola a trojuholník
Priebeh M je parabolický. Priebeh je trojuholník. Plochu berieme vždy z obrazca, kde je parabola. Parabola je čiara 2. stupňa, preto uvažujeme jej plochu (plocha paraboly A = 2/3 x základňa x vzopätie), poradnicu berieme z trojuholníka v mieste pod ťažiskom paraboly.
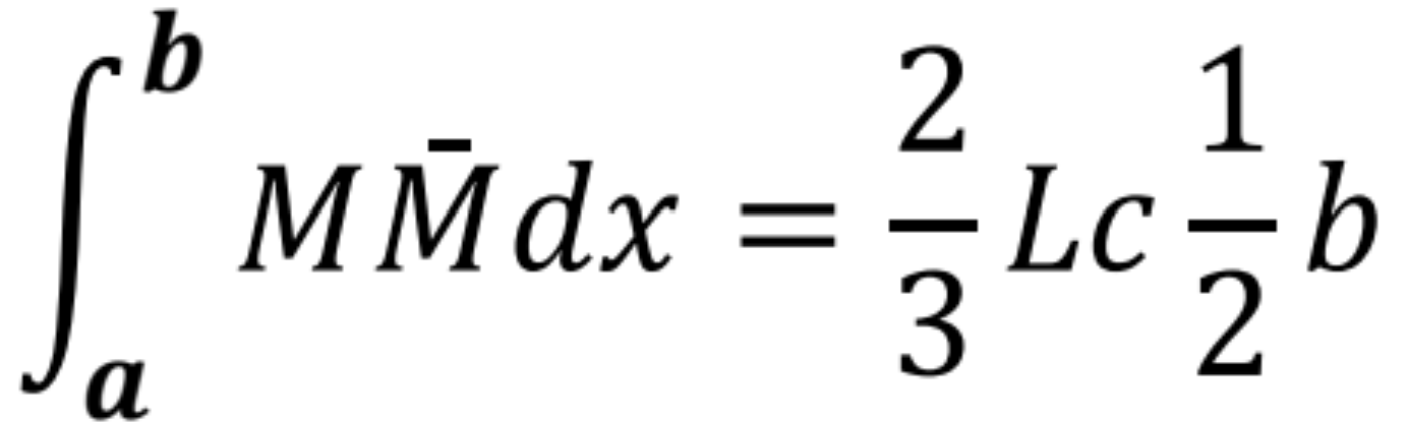
Príklad kombinácie 2 – dva lichobežníky
V príklade kombinujeme dva lichobežníky. V tomto prípade je jedno z ktorého obrazca je plocha. Každý lichobežník si rozdelíme na dva trojuholníky.
Pri lineárnom a konštantnom priebehu si môžeme zvoliť, pri ktorom uvažujeme s plochou. Vyčíslenie integrálu pre momentové obrazce z príkladu 2 je nasledovné:
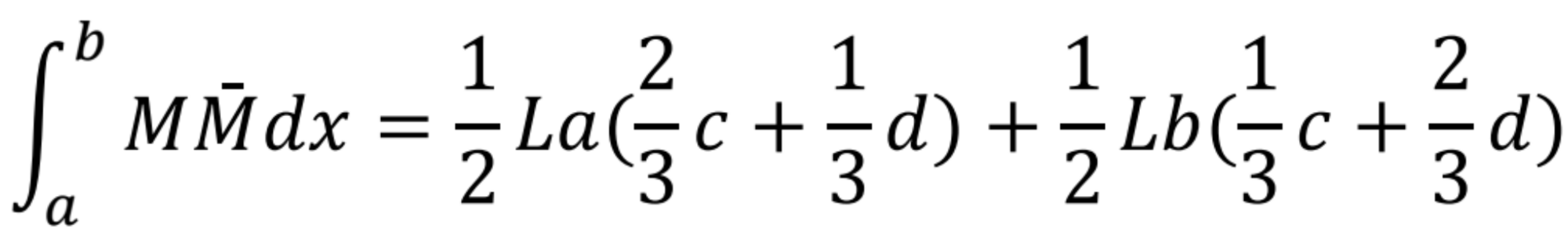
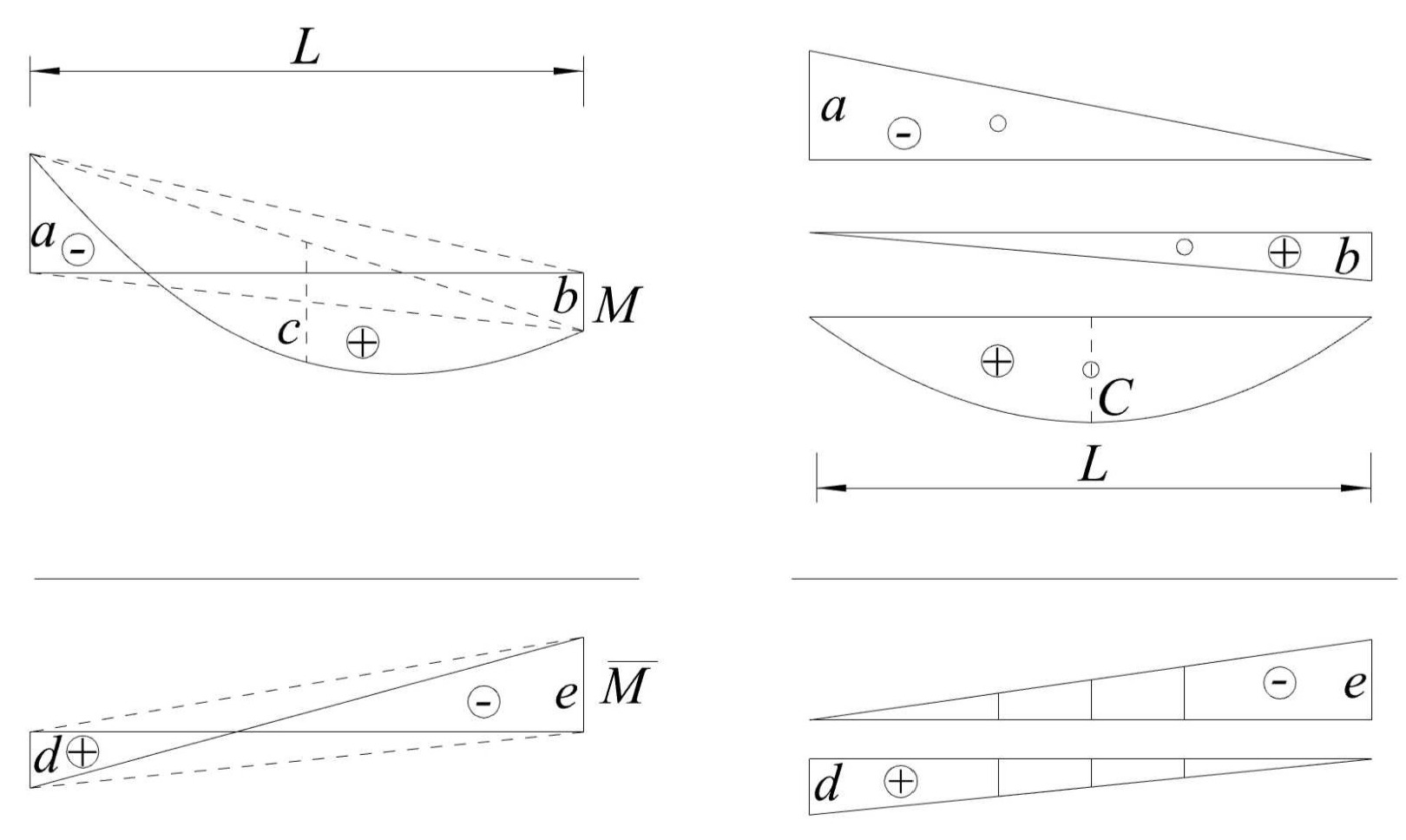
Príklad kombinácie 3
V tomto príklade je priebeh M zložitejší.
Priebeh M – rozdelíme na lichobežník a parabolu 2°. Každý lichobežník si rozdelíme na dva trojuholníky.
Ku každej čiastkovej ploche musí byť priradená poradnica pod jej ťažiskom. Poradnica sa môže skladať aj z viacerých časti. Vyčíslenie integrálu pre momentové obrazce z príkladu 2 je nasledovné:
