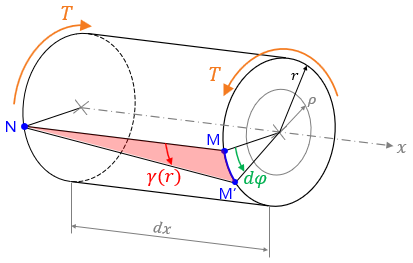
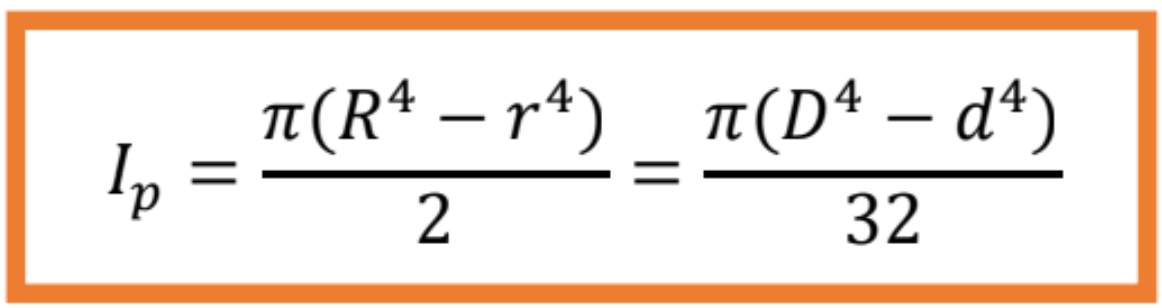Na základe prijatých hypotéz v prierezoch prúta nevznikajú normálové napätia. Dva susedné prierezy vo vzdialenosti dx sa v dôsledku krútiaceho momentu T pootočia o uhol dφ, čím vznikne na povrchoch sústredených valcov skos.
- Skos γ na povrchu valca určíme z pravouhlého trojuholníka NMM':
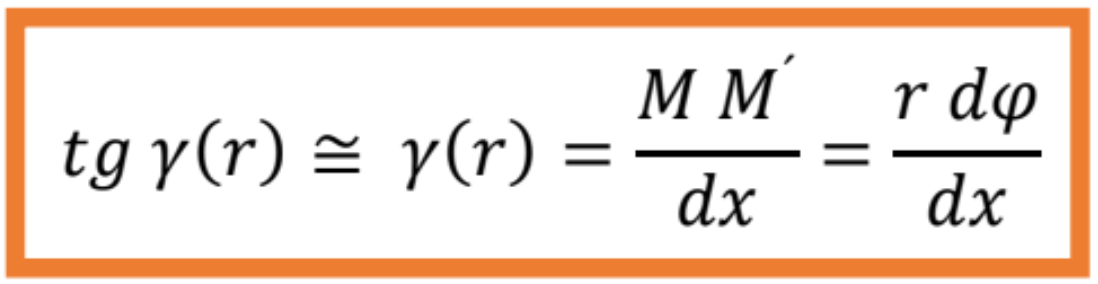
- Pre každý povrch sústredeného valca s polomerom ρ bude skok:
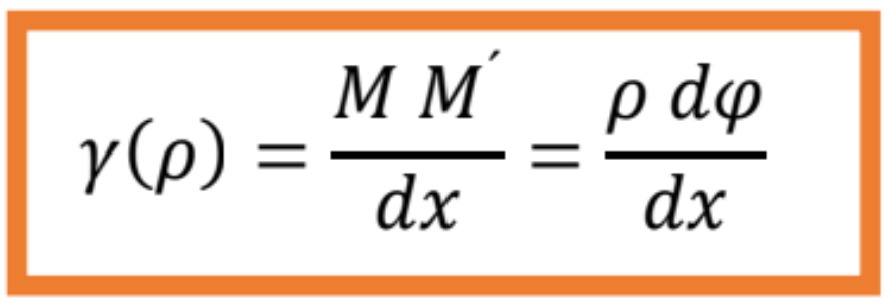
- Skoku odpovedá tangenciálne napätie, ktoré podľa Hookovho zákona vyjadríme nasledovne:
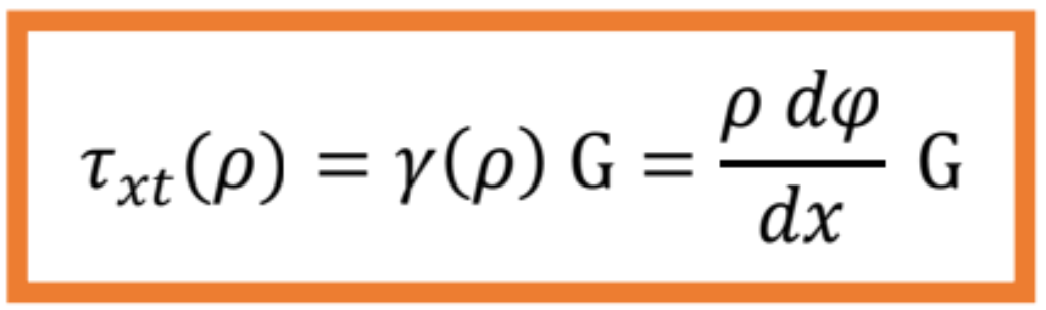
Prvý index označuje normálu, druhý index označuje smer (dotyčnicu).
- Zo vzťahu vyplýva lineárna závislosť napätia od polomeru p.
- Tangenciálne napätie v každom bode prierezu má smer dotyčnice ku kružnici s polomerom p.
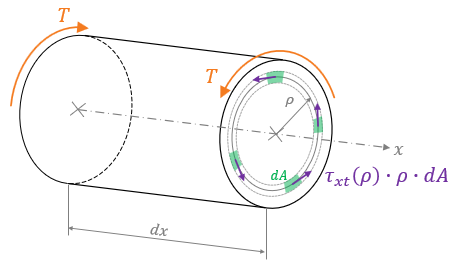
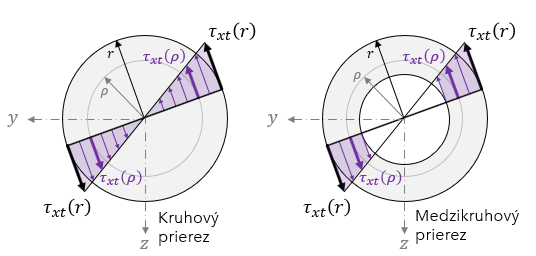
Veľkosť tangenciálneho napätia určíme z podmienok ekvivalencie elementárnych síl a krútiaceho momentu v priereze
- Zo šiestich podmienok ekvivalencie je nenulová iba podmienka.
Ak dosadíme
dostaneme
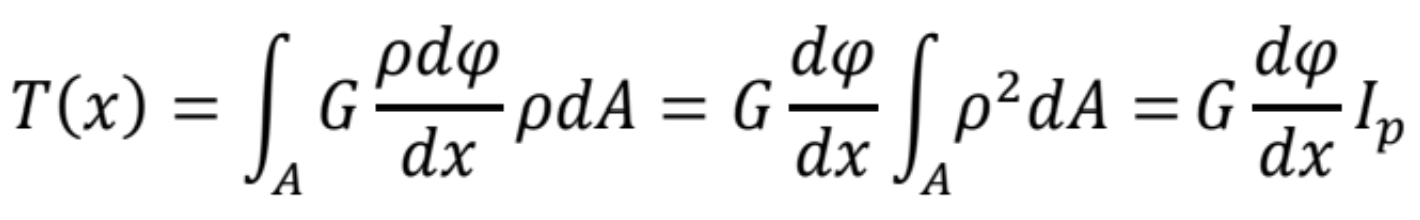
- Tangenciálne napätie je
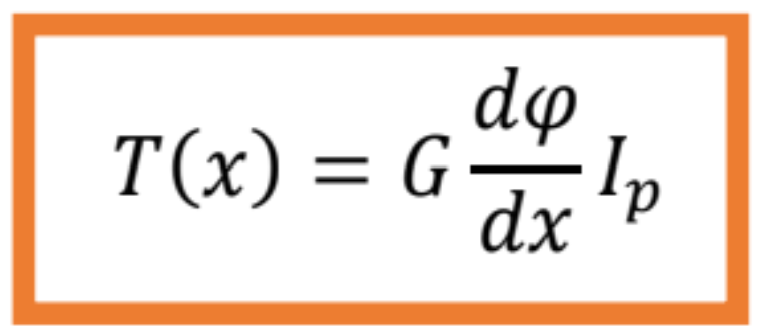
kde
je zmena pootočenia prierezu po dĺžke prúta,
je polárny moment zotrvačnosti.
- Pootočenie (uhol skrútenia) dφ medzi dvomi nekonečne blízkymi prierezmi je
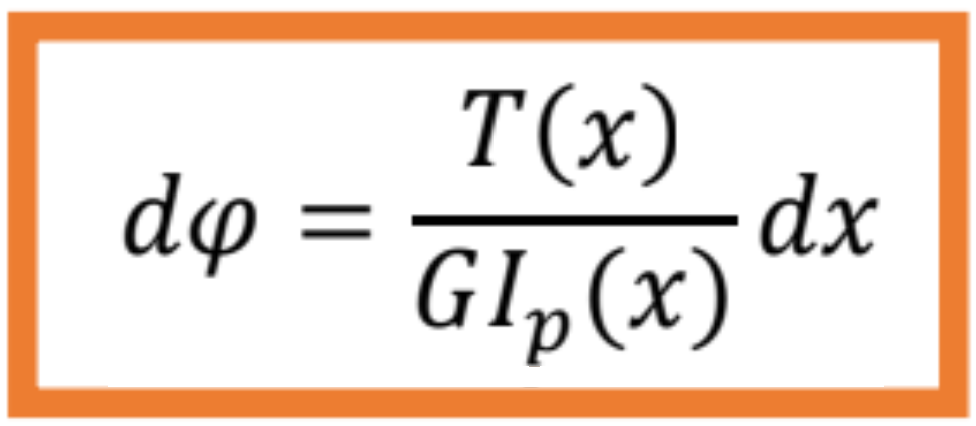
Vzájomné pootočenie dvoch prierezov 
a b
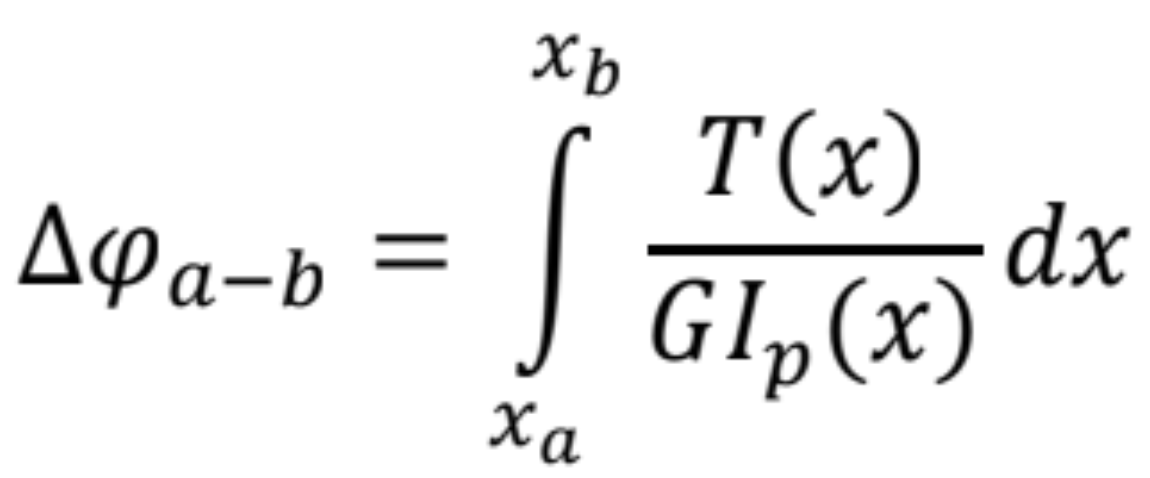
- Pri prizmatických prútoch
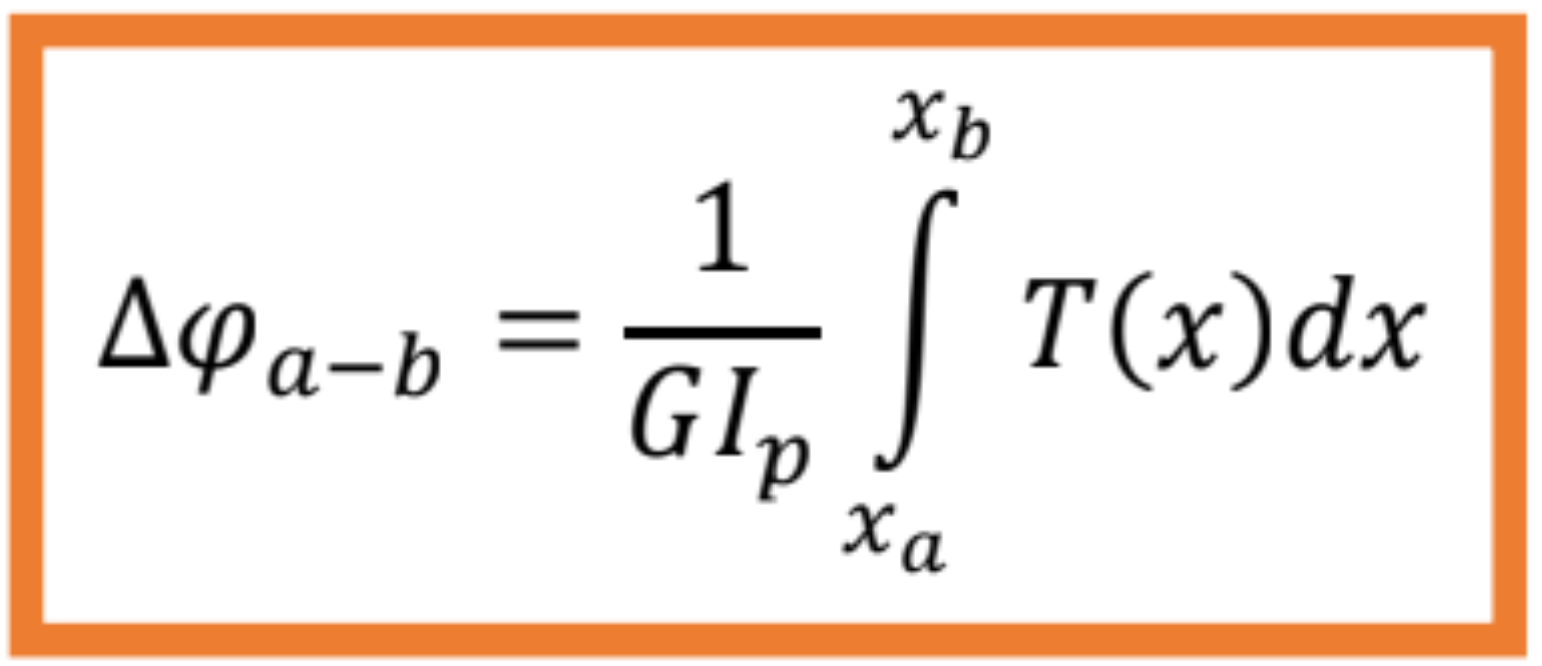
- Súčin GIp sa nazýva tuhosť kruhového prierezu v krútení.
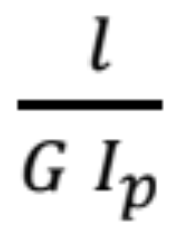je poddajnosť prúta v krútení.
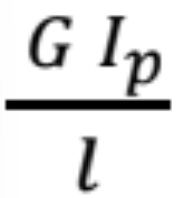je tuhosť prúta v krútení.
- Tangenciálne napätie získame dosadením
do
a dostaneme
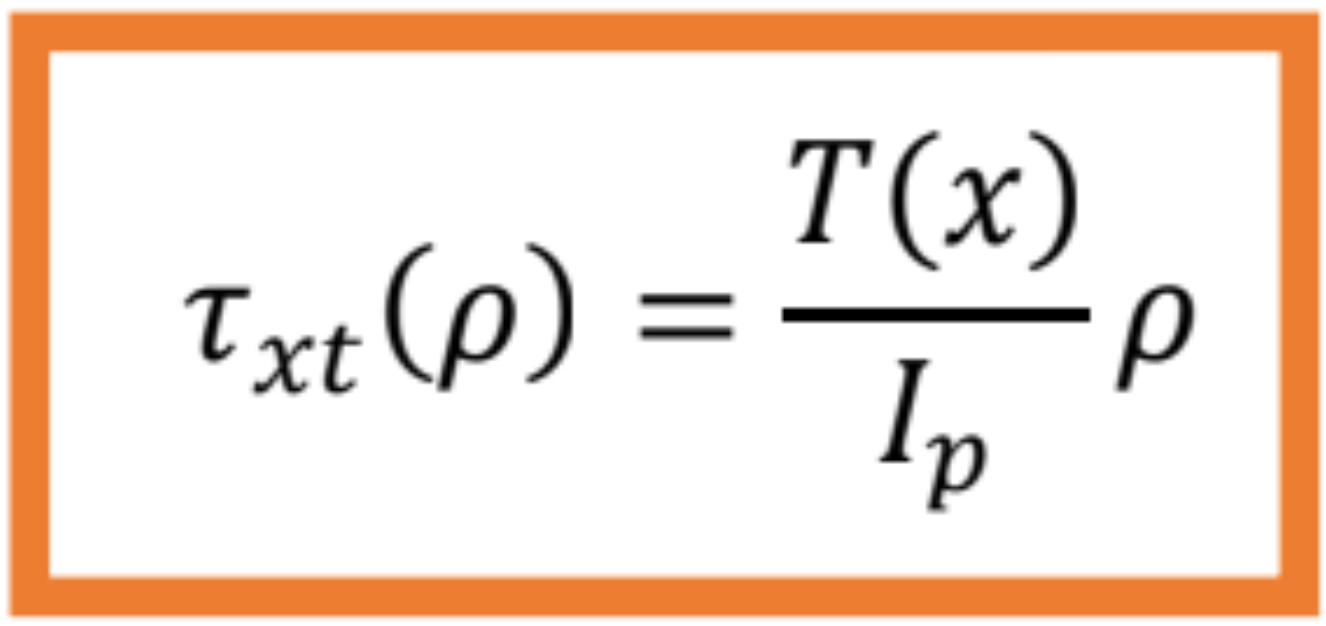
kde polárny moment zotrvačnosti
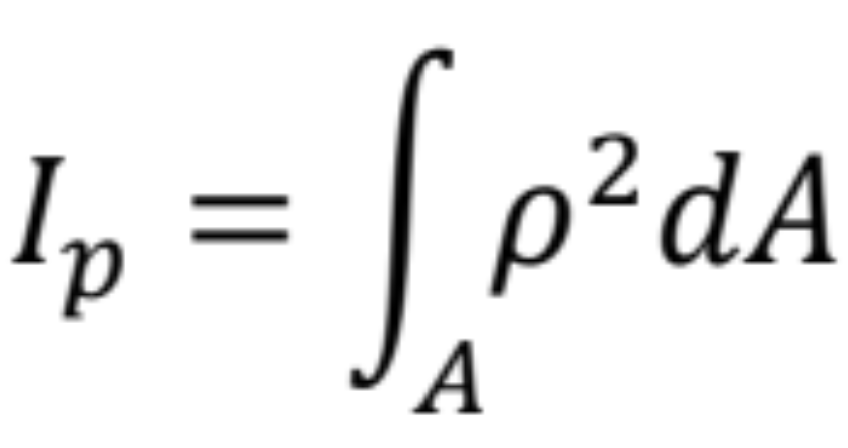
- Maximálne tangenciálne napätie dostaneme na povrchu ak p = r
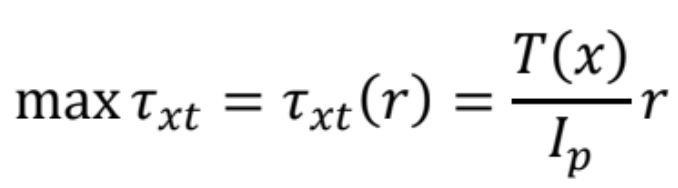
- Polárny moment zotrvačnosti je kvadratický moment plochy prierezu k počiatku sústavy súradníc
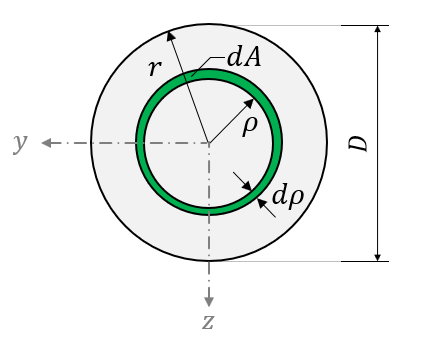
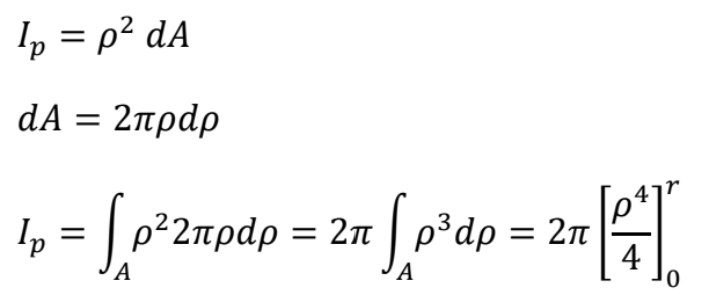
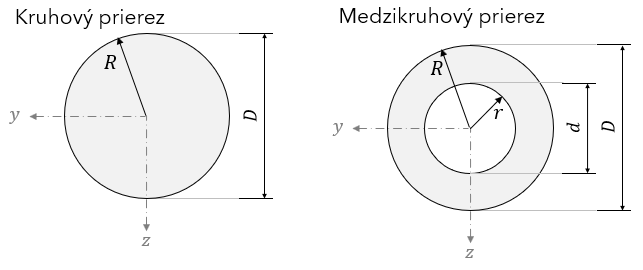
- Polárny moment zotrvačnosti kruhového prierezu
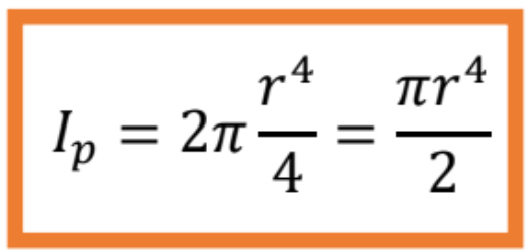
- medzikruhového prierezu
