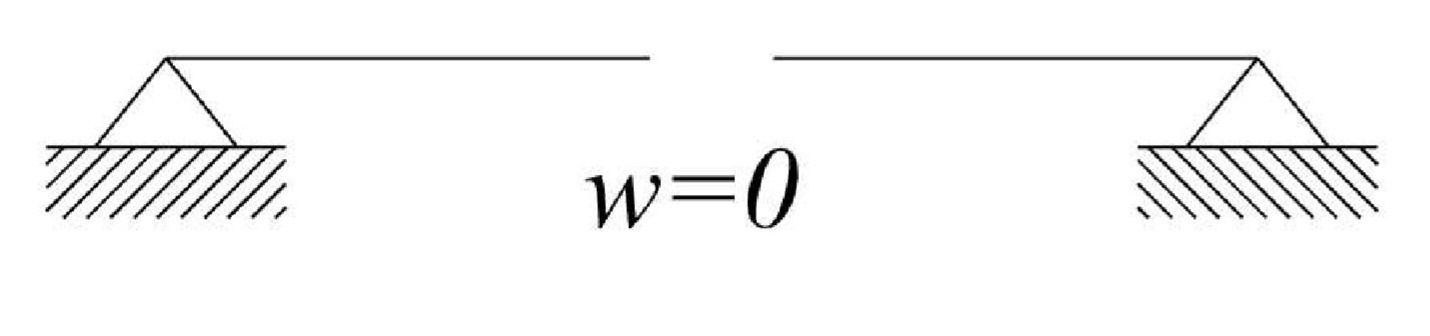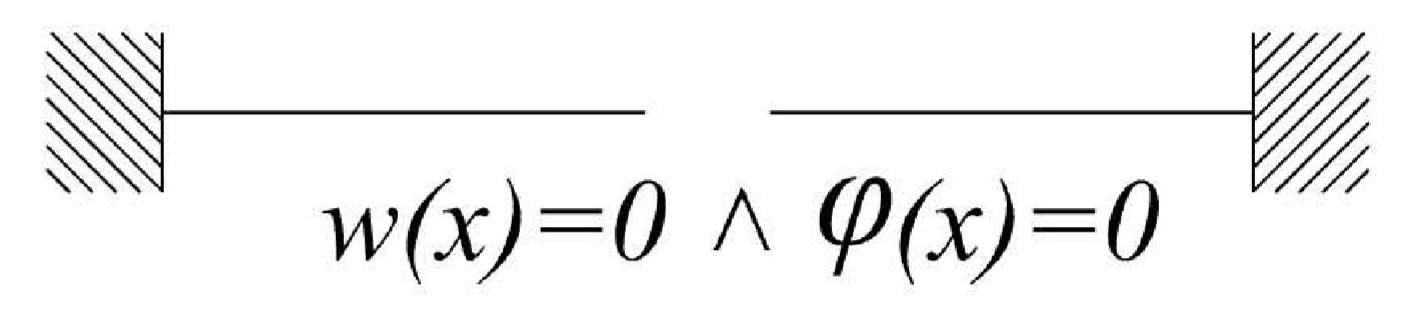Predpokladajme malé deformácie nosníkov, potom si vystačíme s určením zvislých posunov bodov na osi prúta. Pôjde teda o určenie funkcie priehybu w=w(x) pozdĺž osi prúta. Budeme uvažovať len s vplyvom ohybových momentov My(x).
V zmysle Bernoulliho-Navierovej hypotézy sa prierez prechádzajúci bodom m s priehybom w=wm pootočí o uhol φ(x)=φm tak, že pootočenie prierezu je prvou deriváciou ohybovej čiary nosníka:
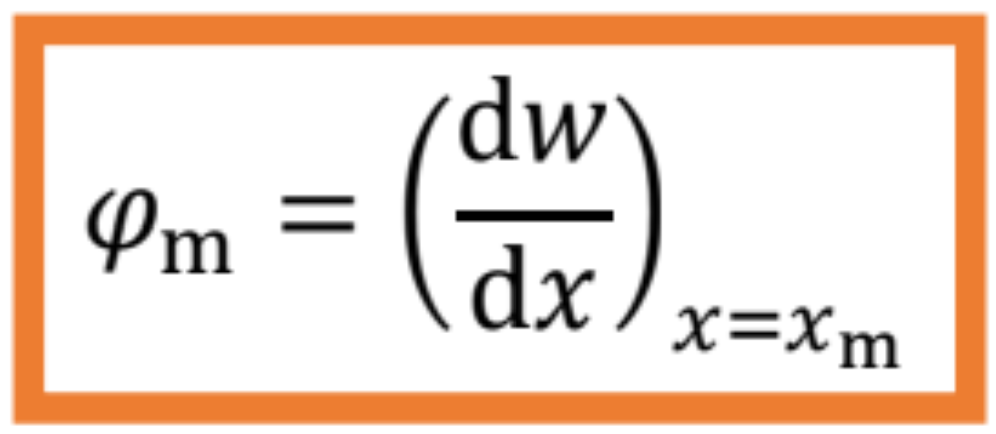
Pri odvodení diferenciálnej rovnice ohybovej čiary vychádzame z rovnice odvodenej pri jednoduchom ohybe,
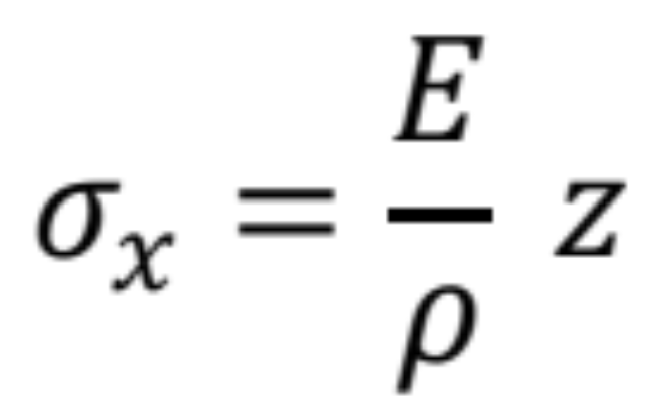
ktorá vyjadruje krivosť prúta.
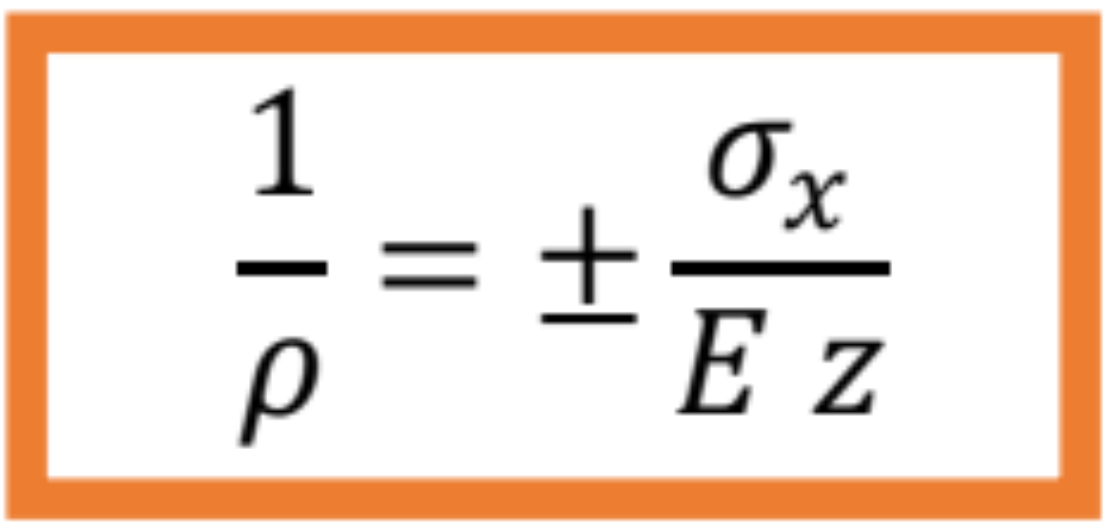
Ak do krivosti prúta dosadíme výraz pre výpočet napätí pri jednoduchom ohybe, dostaneme
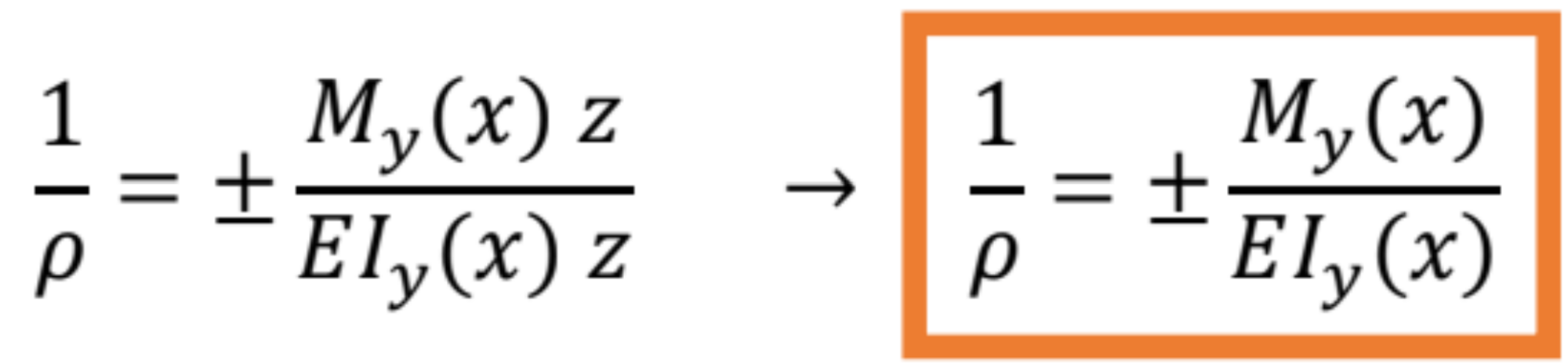
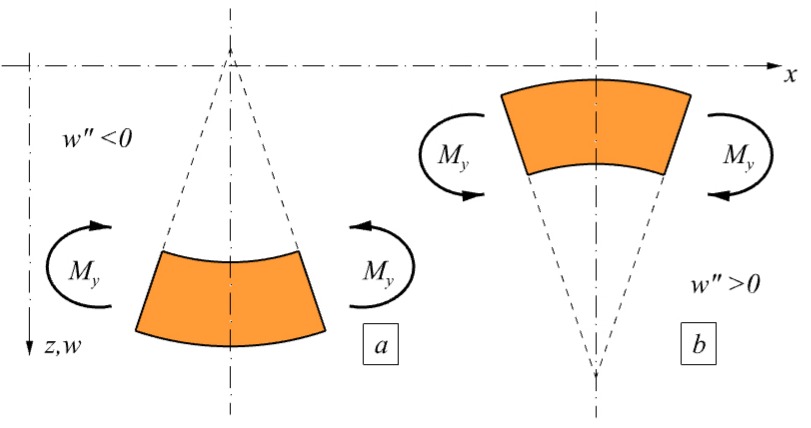
Znamienka v rovnici označujú vzťah medzi súradnicovou sústavou a znamienkovou konvenciou ohybových momentov:
- ak os z aj os w smeruje nadol a ohybové momenty sú kladné a vytvárajú ťah v dolných vláknach nosníka, potom znamienko druhej derivácie funkcie ohybovej čiary je opačné ako znamienko ohybového momentu,
- ak kladné ohybové momenty vytvárajú ťah v horných vláknach nosníka, je znamienko druhej derivácie zhodné so znamienkom ohybového momentu.
Vo zvolenom súradnicovom systéme teda platí
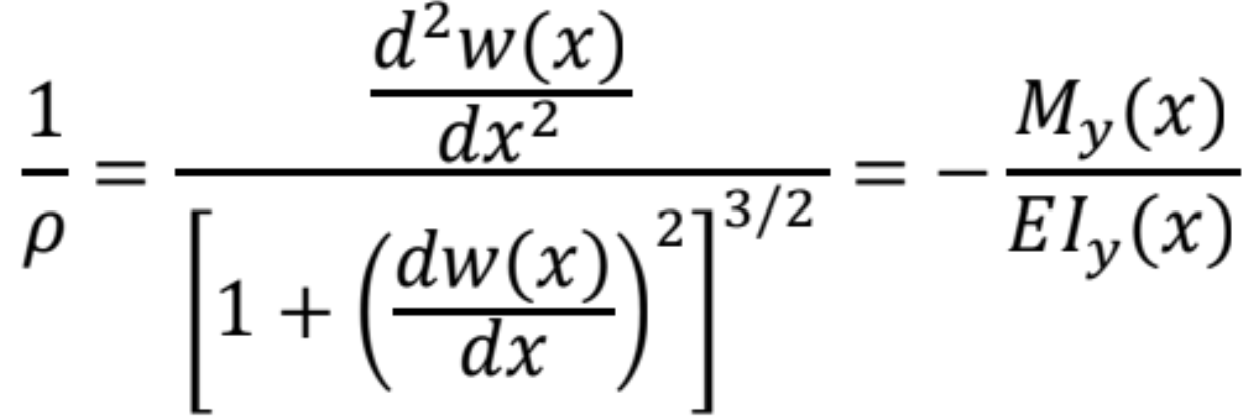
- V prípade predpokladu veľmi malých priehybov nosníka môžeme deriváciu priehybovej funkcie v menovateli oproti 1 zanedbať a tak dostaneme
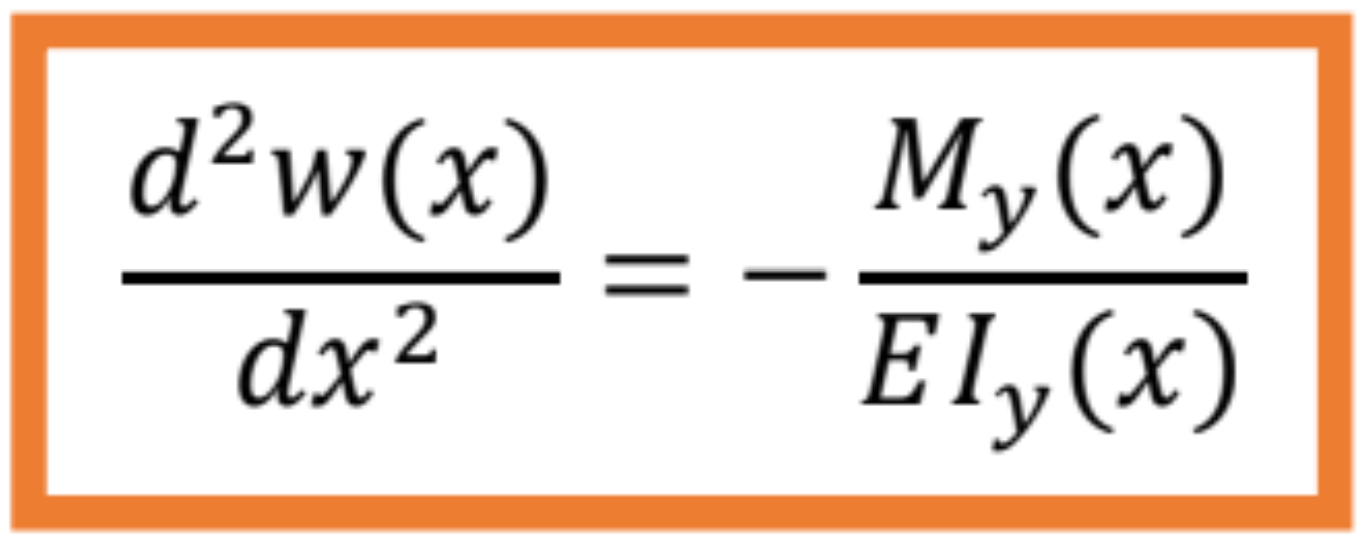
- Ak uvažujeme nosník, ktorého priečny rez sa po dĺžke prúta mení, dostaneme komplikovanú diferenciálnu rovnicu, ktorej riešenie je zložité, alebo nemožné.
Určte priehybovú funkciu nosníka s konštantným prierezom
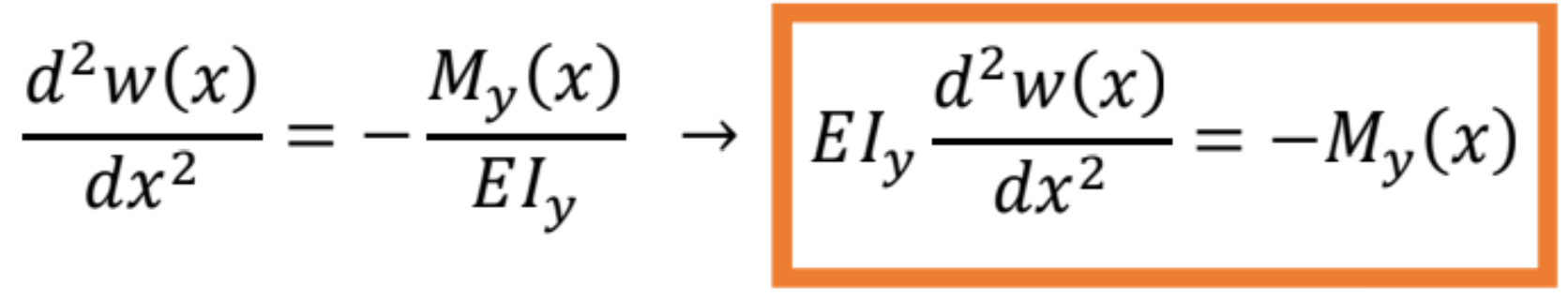
Ktorú môžeme ľahko integrovať
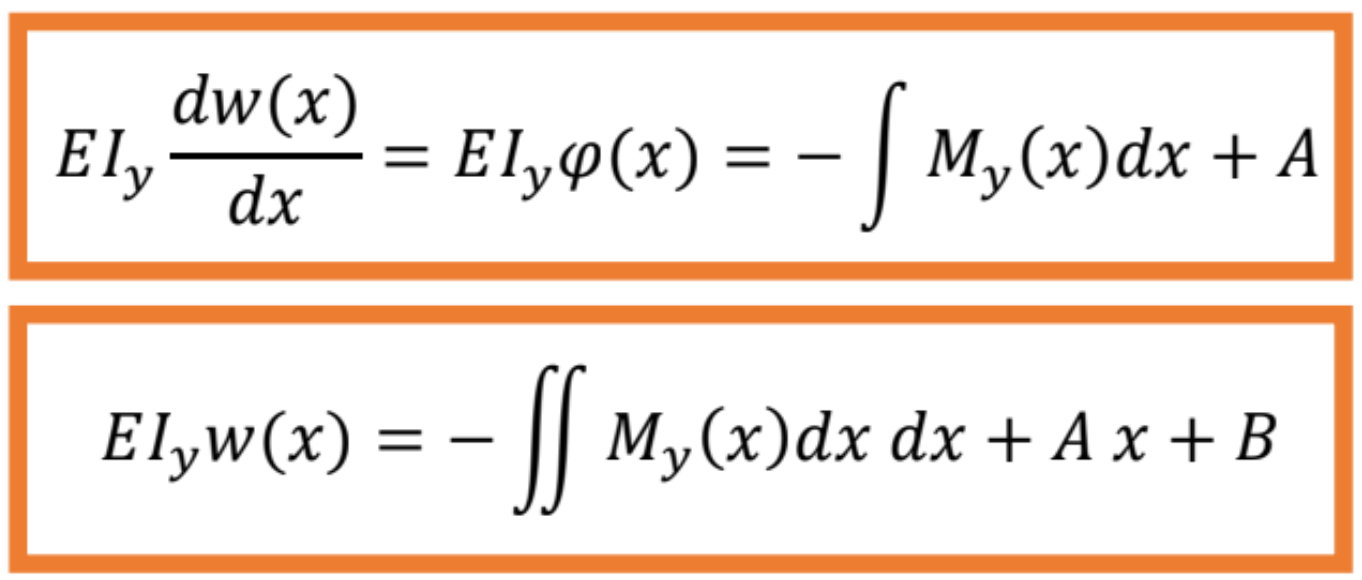
Pre x∈〈0, L〉. Integračné konštanty určíme z deformačných okrajových podmienok, ktoré súvisia s podopretím prúta:
- Ak je prút v mieste x kĺbovo, alebo posuvne kĺbovo podopretý, tak w(x)=0.
- Ak je prút v mieste x votknutý, tak
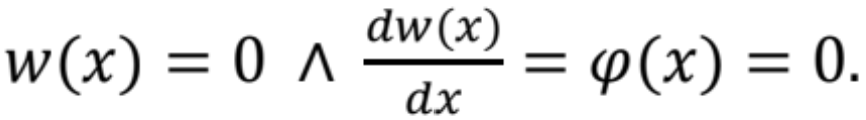
V prípade rozdelenia prúta na n častí, pre každý j-tý úsek platí
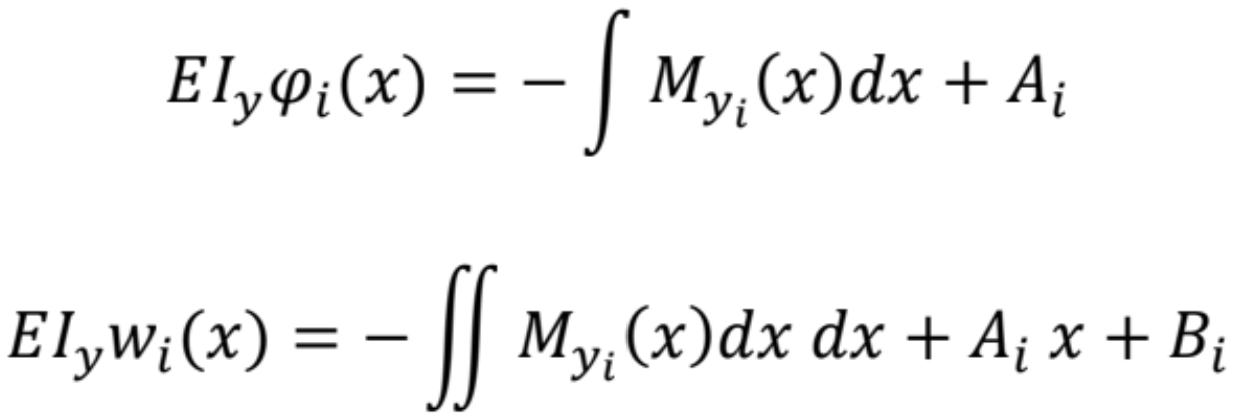
a integračné konštanty určíme z deformačných okrajových podmienok a podmienok spojitosti jednotlivých úsekoch.