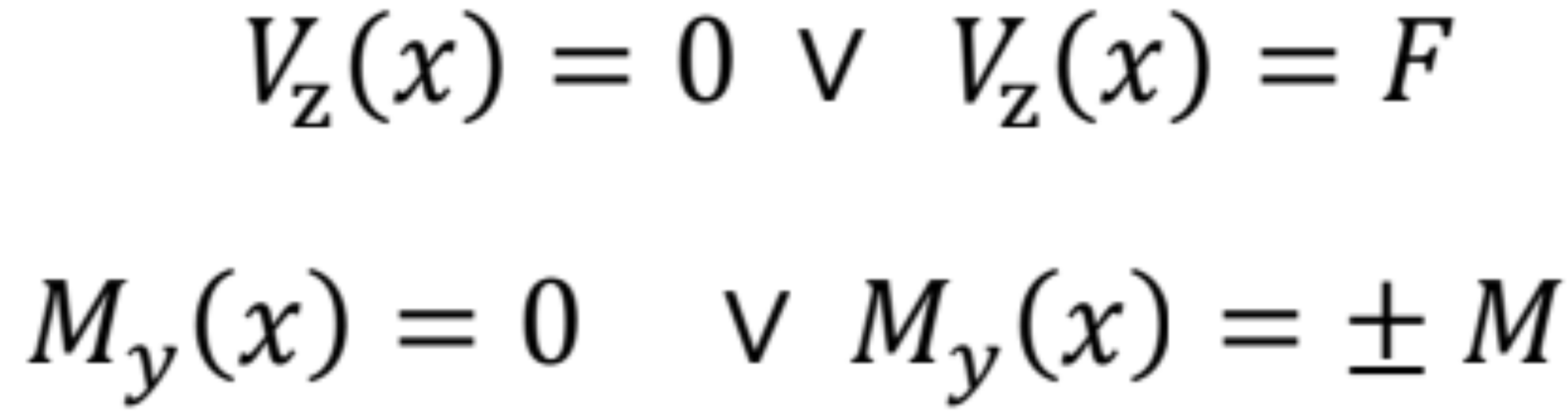Pri odvodení rovnice v modifikovanom tvare dvakrát zderivuje ohybovú čiaru nosníka:
![]()
Podľa Schwedler-Žuravského vety platí:
![]()
Dosadením tohto výrazu do predchádzajúceho dostaneme diferenciálnu rovnicu ohybovej čiary nosníka v modifikovanom tvare.
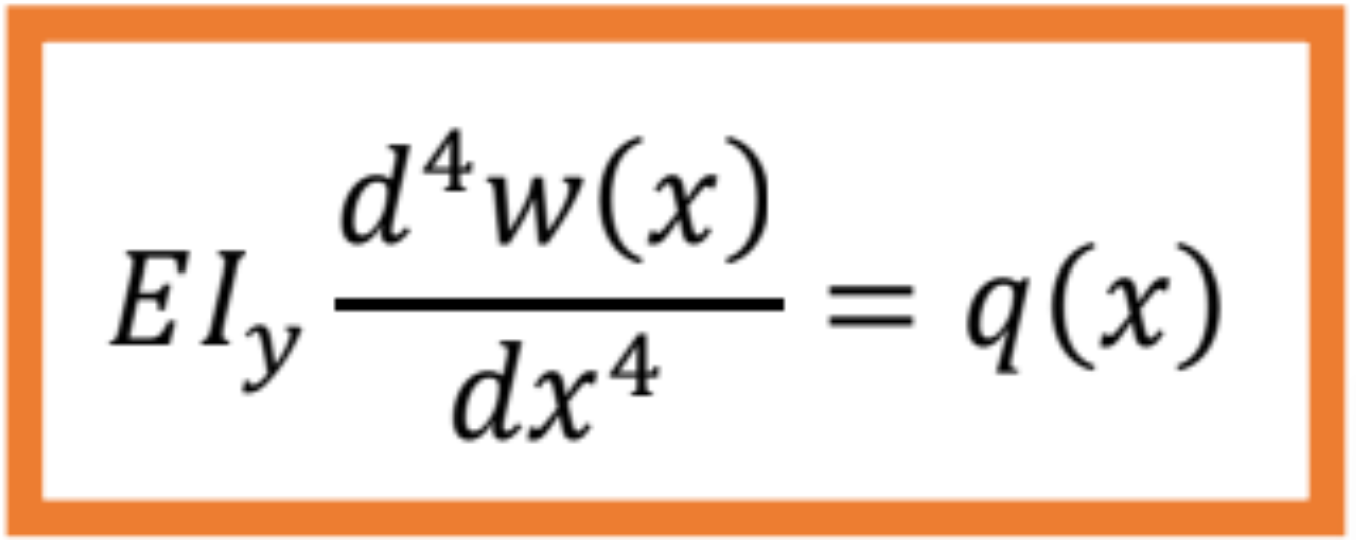
Postupnou integráciou dostaneme:
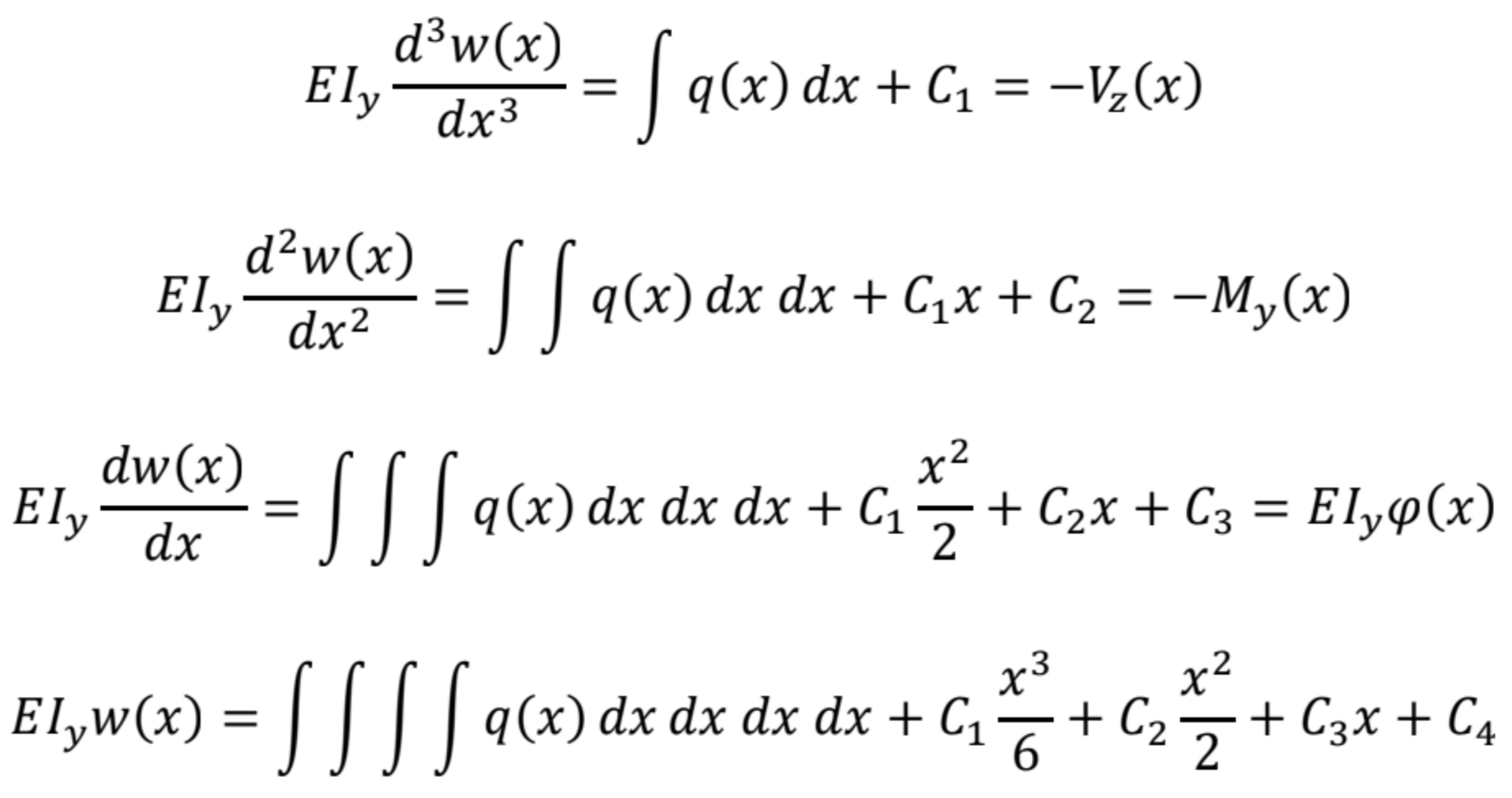
Integračné konštanty dostaneme z dvoch statických a dvoch deformačných (kinematických) okrajových podmienok.
Deformačné (kinematické) okrajové podmienky sú podľa typu uloženia:
- Ak je prút v mieste x kĺb, alebo posuvný kĺb, tak
![]()
- Ak je prút v mieste x votknutý, tak
![]()
Statické okrajové podmienky sú podľa typu uloženia:
- Ak je prút v mieste x kĺb, alebo posuvný kĺb, tak
![]()
- Ak je prút v mieste x nepodopretý – s voľným koncom, tak