?ohrova analógia výpočtu deformácii pružných prútov je založená na analógii dvoch diferenciálnych rovníc a to:
- Diferenciálnej rovnice ohybovej čiary nosníka konštantného prierezu
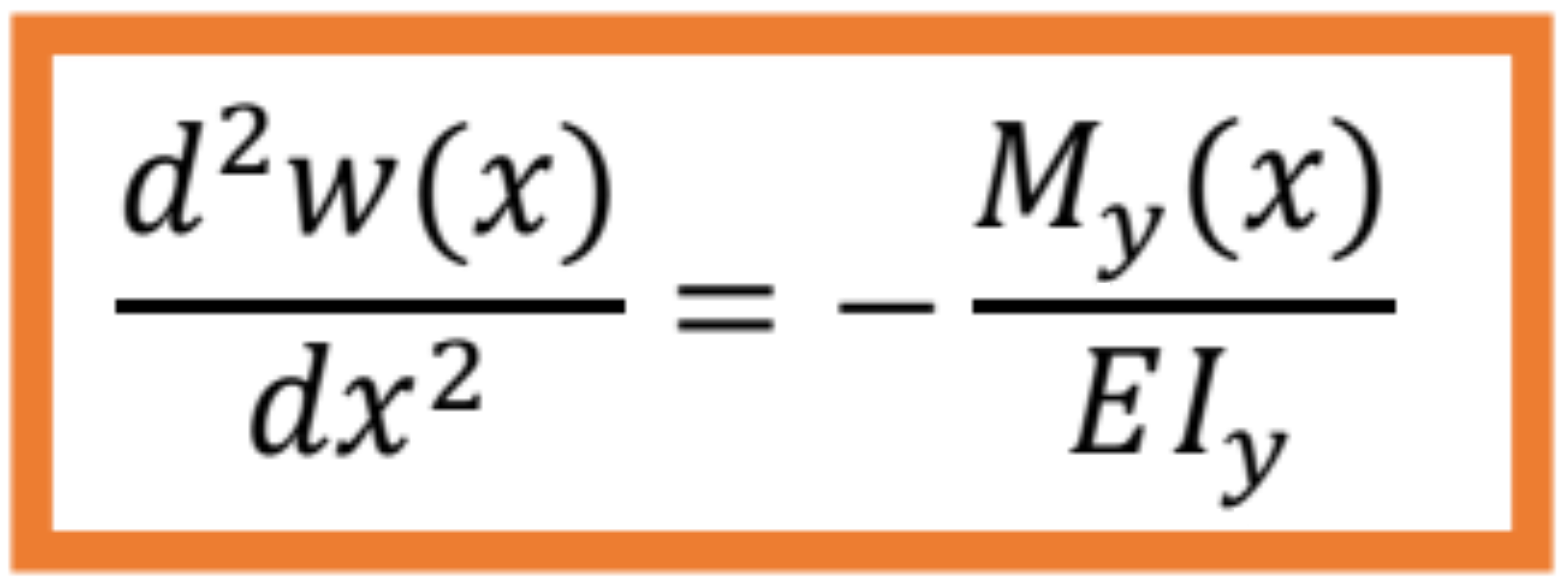
- a Schwedler-Žuravského vety, vyjadrujúcej vzťah medzi ohybovým momentom a zaťažením prúta.
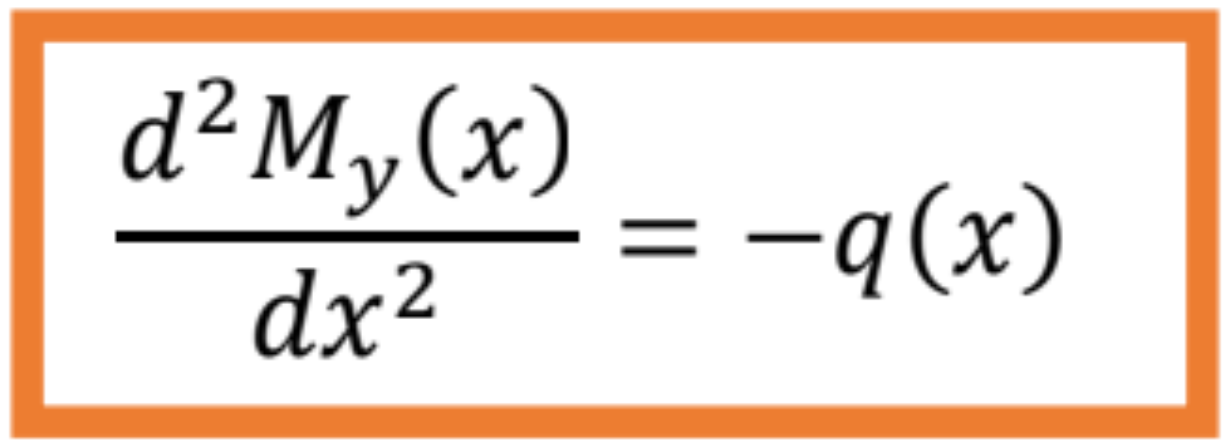
Z matematického hľadiska môžeme obe diferenciálne rovnice vyjadriť v tvare
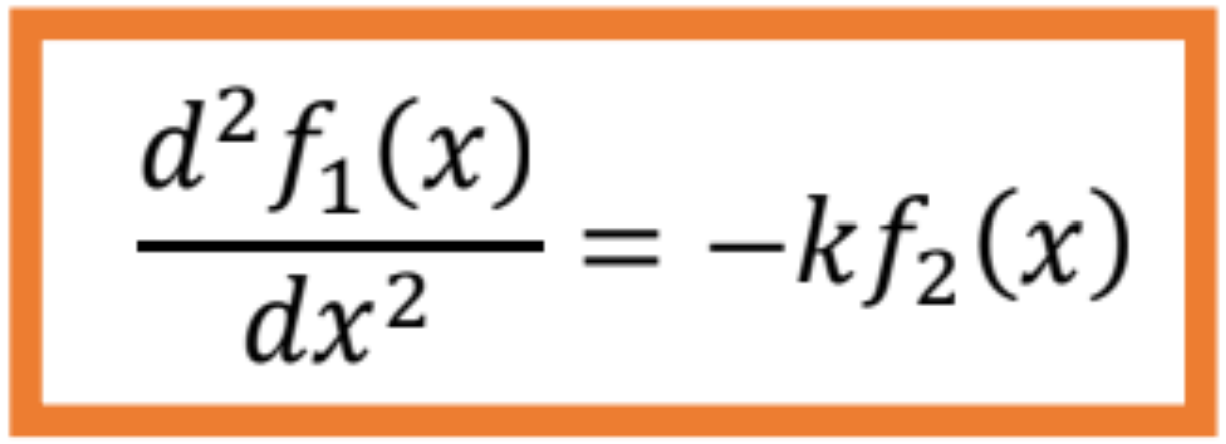
kde 
,
sú funkcie premennej x a k je konštanta.
Porovnajme teraz riešenie oboch diferenciálnych rovníc
- zo statiky vieme, že po Schwedler-Žuravského vety dostaneme priečnu silu V(x) a po druhej integrácii ohybový moment My(x),
- po prvej integrácii ohybovej čiary nosníka dostaneme pootočenie nosníka φ(x) a po druhej integrácii priehyb nosníka w(X).
Uvažujme pružný prút zaťažený fiktívnym zaťažením, ktoré v zhode s rovnicou ohybovej čiary nosníka by predstavovalo funkciu ohybového momentu My(x) deleného tuhosťou prúta EIy.
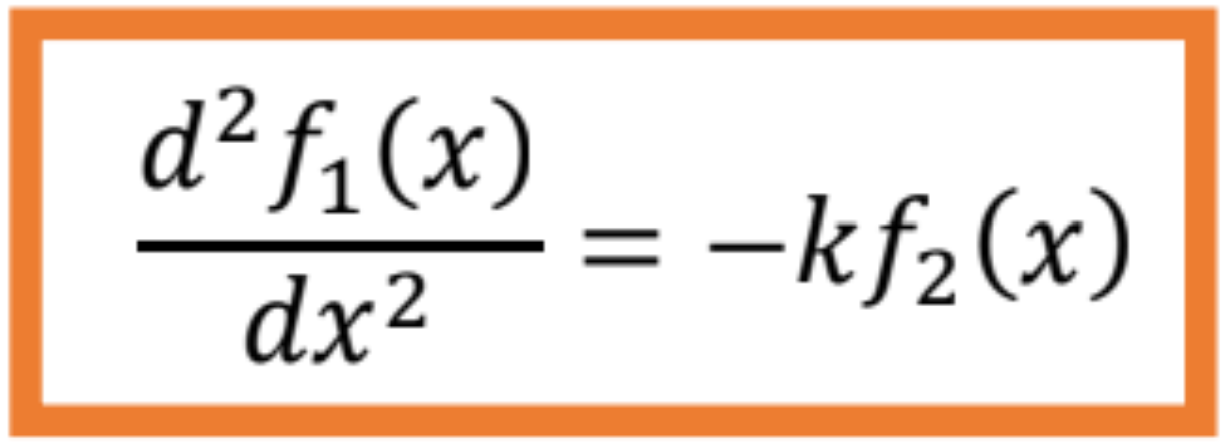
Uvážme teraz, že fiktívne zaťaženia dosadíme do Schwedler-Žuravského vety. Ak ide o fiktívneho zaťaženia, tak aj vnútorné sily budú fiktívne, čím dostaneme rovnicu:
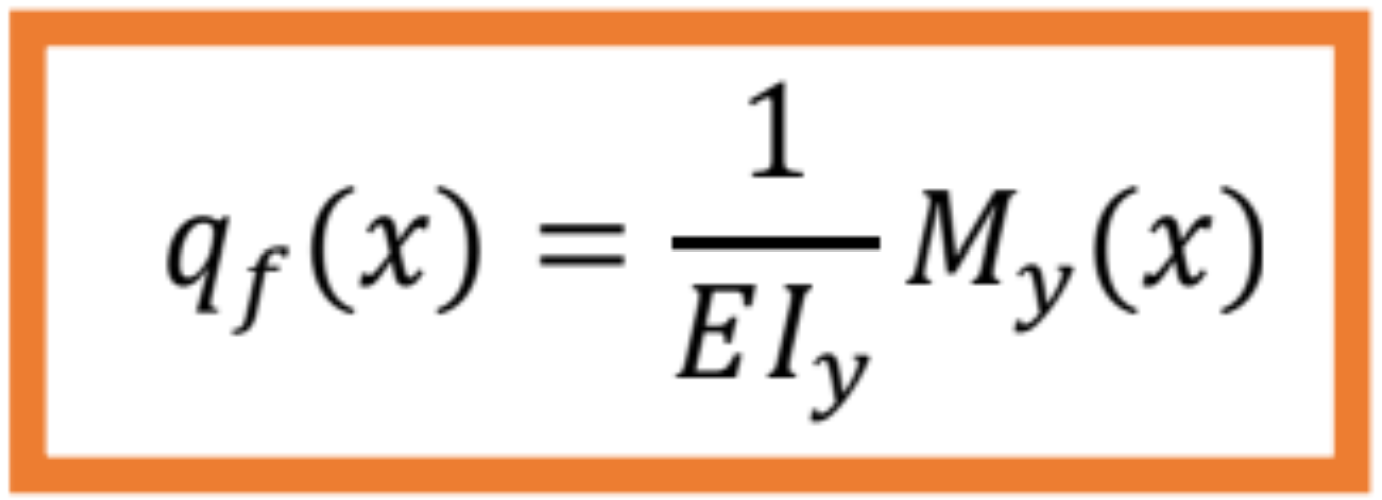
Po prvej integrácii dostaneme fiktívnu priečnu silu 
a po druhej integrácii fiktívny ohybový moment 
.
Schematicky vyjadrené úvahy:
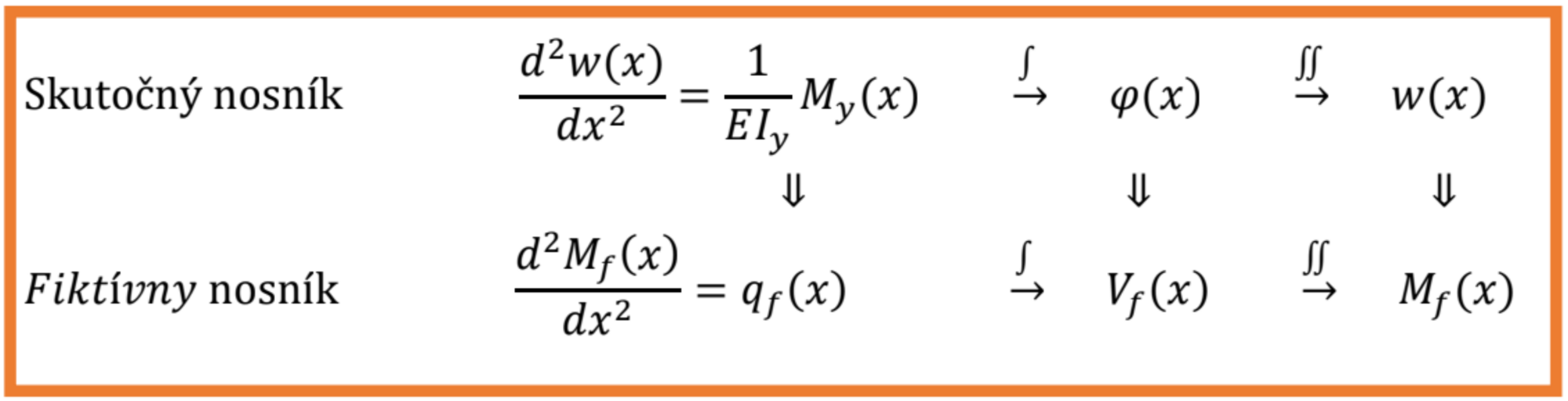
Existuje teda analógia medzi:
- potočením φ(x) na skutočnom nosníku a fiktívnou priečnou silou 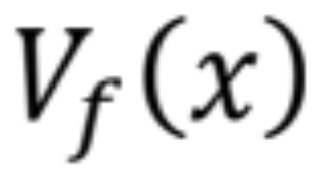na fiktívnom nosníku od fiktívneho zaťaženia,
- priehybom w(x) na skutočnom nosníku a fiktívnou momentom 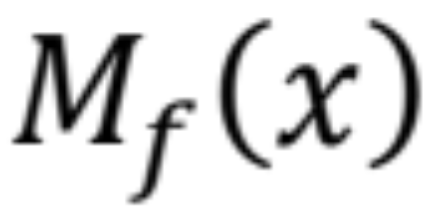na fiktívnom nosníku od fiktívneho zaťaženia,
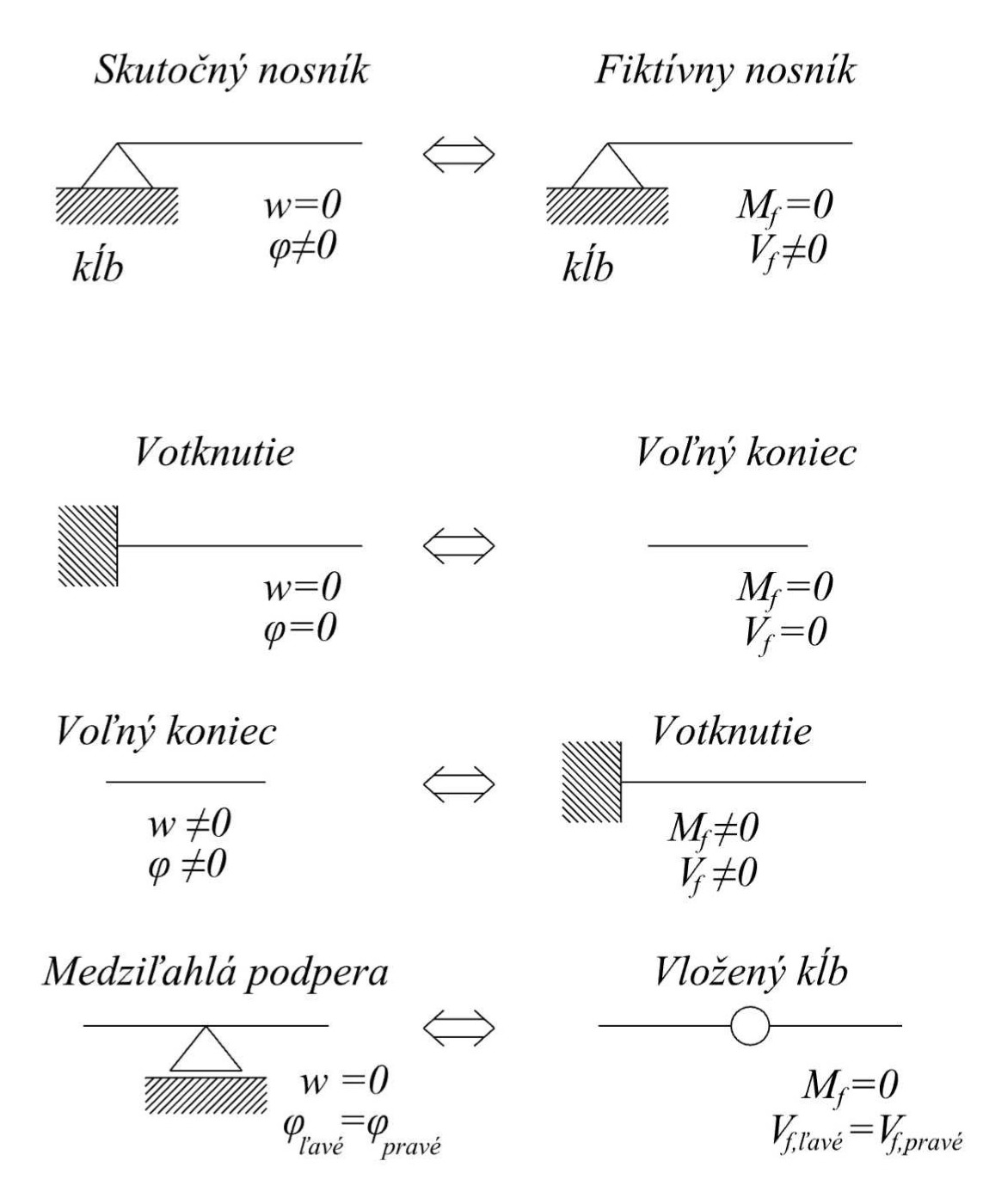
Okrajové podmienky pre vytvorenie fiktívnych nosníkov:
Skutočný nosník Fiktívny nosník
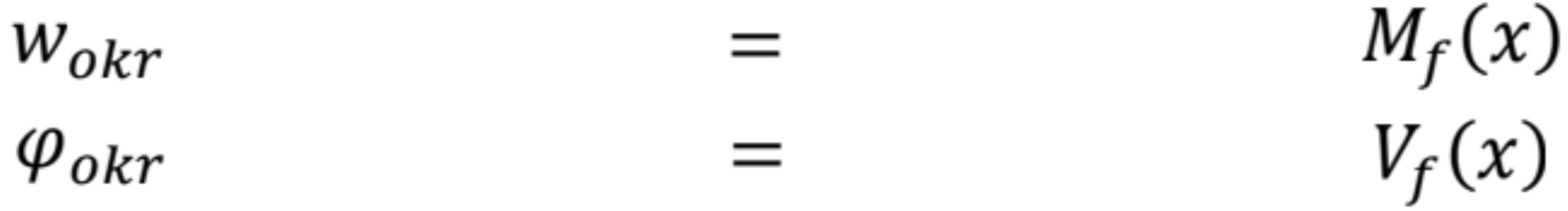
Fiktívne väzby pre rôzne typy okrajových podmienok
Postup pri určovaní funkcií pootočení a priehybov prúta pomocou Mohrovej analógie:
- vypočítame priebehy ohybových momentov na skutočnom nosníku od skutočného zaťaženia,
- určíme intenzitu fiktívneho zaťaženia tým, že funkciu skutočného ohybového momentu delíme tuhosťou EIy,
- vytvoríme fiktívny nosník a zaťažený fiktívnym zaťažením,
- určíme fiktívne priečne sily 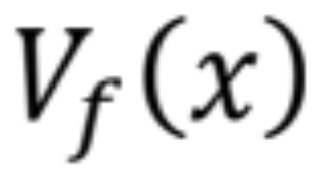, čo predstavujú pootočenia osi prúta na skutočnom nosníku,
- určíme fiktívne ohybové momenty 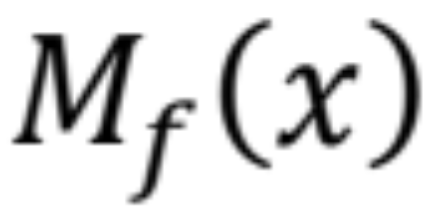, čo sú vlastne priehyby osi prúta na skutočnom nosníku,
Ak je ohybový moment kladný, fiktívne zaťaženie smeruje zhora nadol.
