Napätosť v bode sme skúmali v karteziánskej sústave súradníc s vodorovnými a zvislými osami. Podobne ako pri vektoroch, platí aj pre tenzor napätí, že veľkosť orientovanej veličiny závisí od voľby sústavy súradníc. Pre prípad rovinnej napätosti budeme skúmať, ako sa mení veľkosť napätí v pootočenej sústave súradníc. Uvažujeme sústavu súradníc xz s osou z smerujúcou smerom dole.
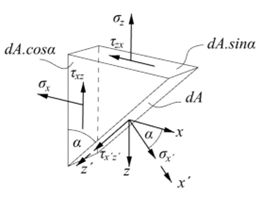
Na rovnovážny diferenciálny element pôsobia napätia v rovine vo vodorovnom a zvislom smere. Diagonálny rez definuje pootočenú sústavu súradníc x’z’, v ktorej pôsobí normálové napätie σx' a šmykové napätie τx'z'. Diagonálny rez má plochu dA. Všetky napätia na skosenom diferenciálnom elemente musia byť v rovnováhe. Zapíšeme rovnováhu síl v smere x a z
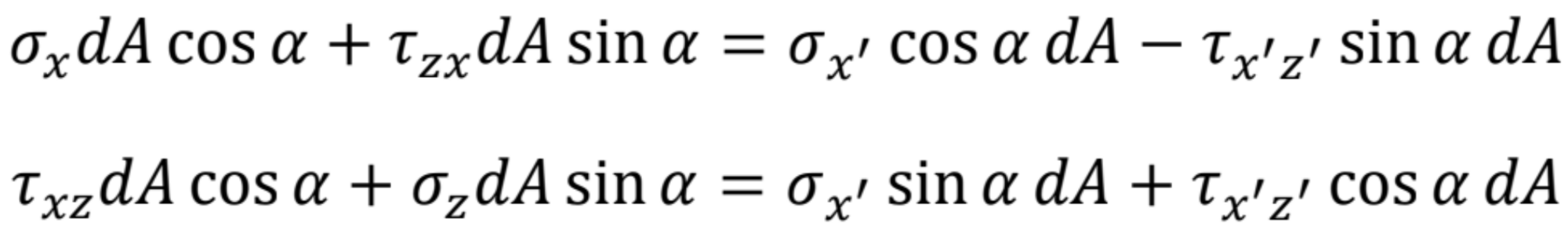
Plocha dA sa vykráti a dostaneme rovnice na rovnovážnom elemente
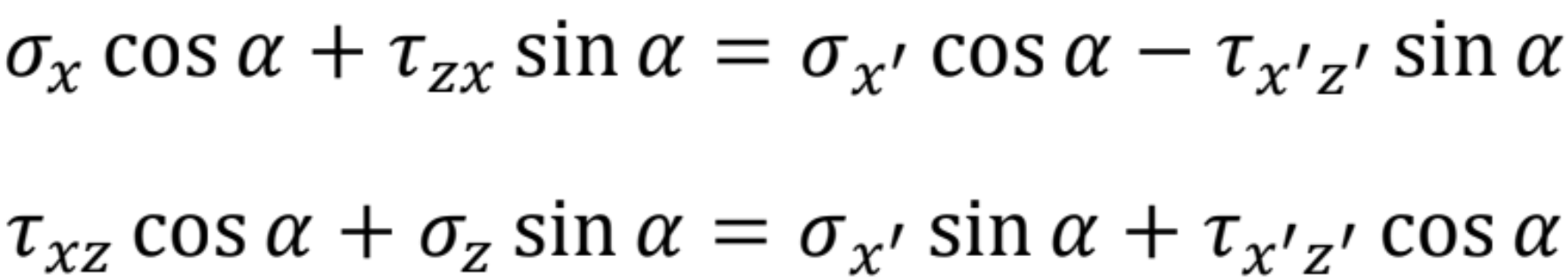
Riešením sústavy rovníc získame napätia pôsobiace v reze
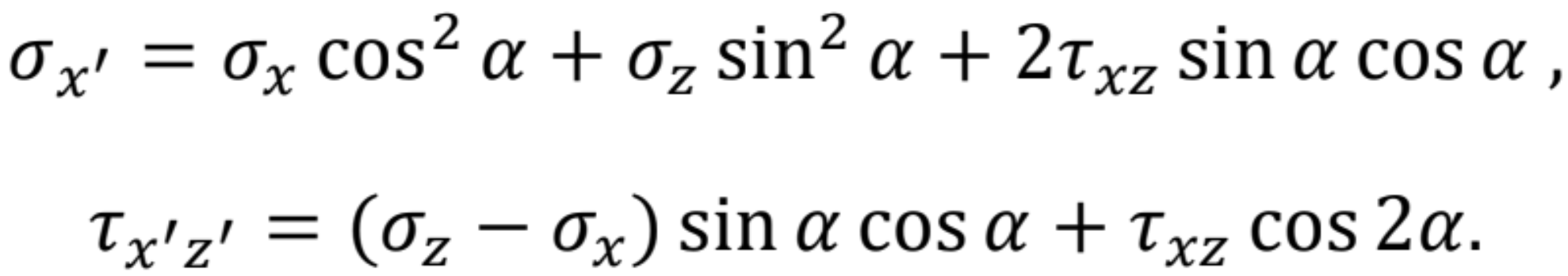
Riešenie x': Prvú rovnicu násobíme cos , druhú sin , rovnice sčítame a upravíme
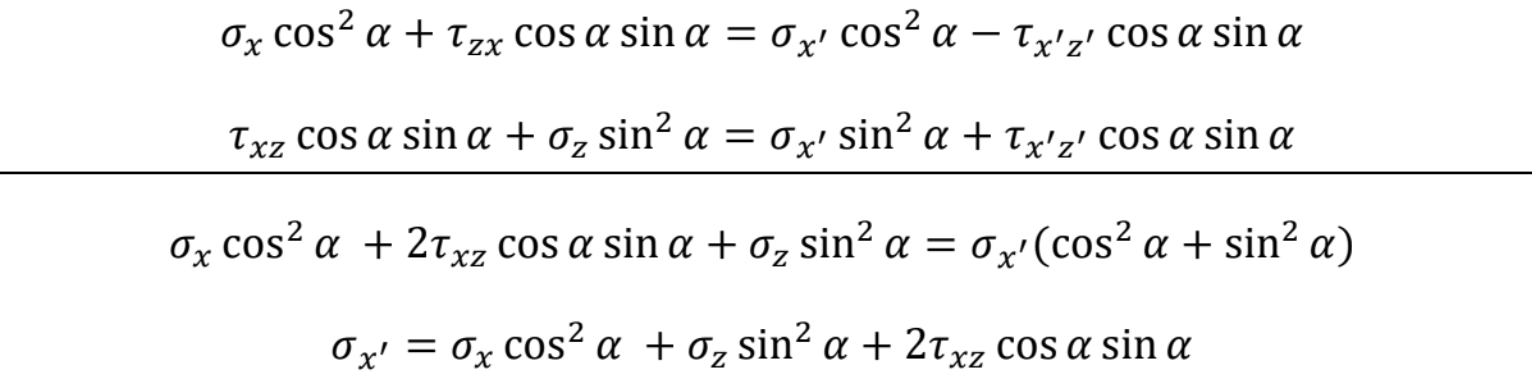
Riešenie x'z': Prvú rovnicu násobíme -sin , druhú cos , rovnice sčítame a upravíme
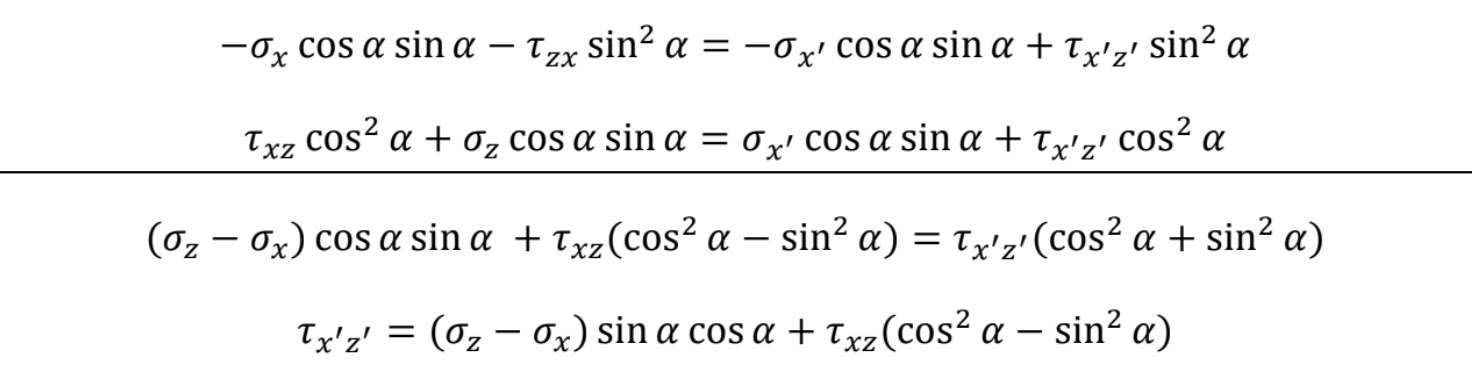
pričom cos2α – sin2α = cos2α
Pre úplné opísanie stavu napätosti v pootočenej sústave súradníc potrebujeme normálové napätia σz' v smere z’. Namiesto odvodenia na diferenciálnom elemente ich nájdeme ako normálové napätia na ploche pootočenej o α + 90°
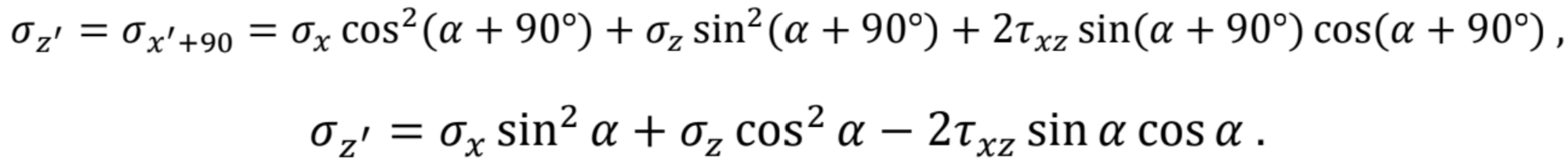
Všetky tri vzťahy pre σx', σz', τx'z' môžeme zapísať jednou maticovou rovnicou
Ak definujeme transformačnú maticu ako
môžeme zapísať predchádzajúci maticový vzťah ako
Použitím trigonometrických identít 
môžeme zapísať vzťahy pre transformáciu zložiek tenzora napätosti aj nasledovne
Poznámka k priamkovej napätosti: Stav priamkovej napätosti existuje len v smere spoločnej priamky zväzku rovín, na ktoré nepôsobia napätia. Pri odčítaní zložiek napätí v sústave súradníc ľubovoľne pootočenej vo zvolenej rovine, budú zložky σx', σz', τx'z' nenulové. Zo transformačných vzťahov je zrejmé, že aj v prípade že 
výsledné napätia v pootočenej sústave súradníc nebudú nulové.
Transformácia zložiek tenzora napätí v priestore
Transformačnú maticu pre rovinný stav napätosti môžeme vyjadriť na základe uhlov, ktoré vzájomne zvierajú osi pôvodnej a pootočenej sústavy súradníc. Prvky transformačnej matice sú smerové kosínusy orientovaných uhlov, ktoré jednotlivé osi zvierajú. Smerový kosínus uhla, ktorý zviera os x’ s osou x zapíšeme ako cos αx'x .
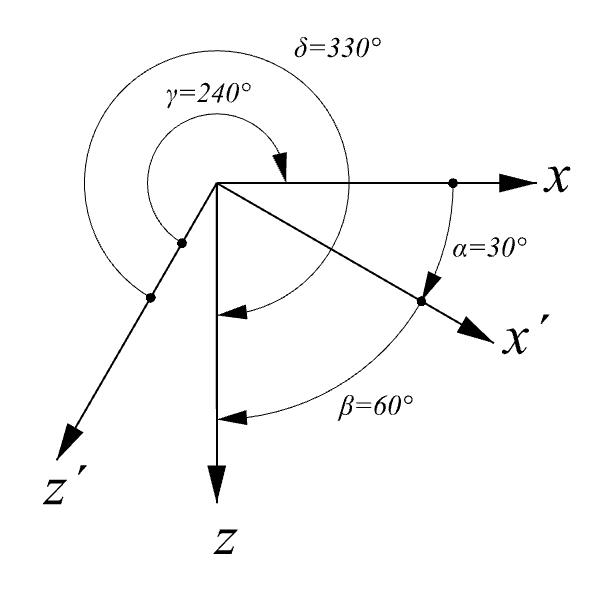
Pre hodnoty uhlov podľa predchádzajúceho obrázku je číselné vyhodnotenie transformačnej matice
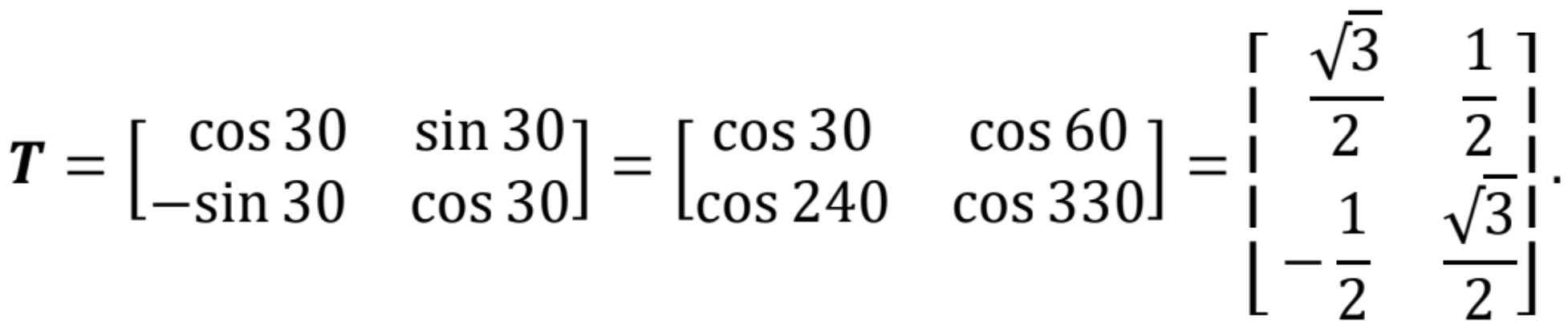
Transformačnú maticu definovanú na základe smerových kosínusov vzájomných uhlov medzi súradnicovými osami, môžeme zovšeobecniť pre trojrozmernú sústavu súradníc v priestore takto
Potom sa transformácia tenzora napätí pre priestorovú napätosť vykoná podľa vzťahu 
