Extrémy normálových napätí
V praxi nás zaujíma aké maximálne hodnoty napätí sa v telese môžu vyskytnúť, pretože to sú hodnoty napätí, ktorým musí materiál odolať. Každý materiál má určitú únosnosť, ktorá pri návrhu konštrukcií nesmie byť prekročená. Ako sme si ukázali, veľkosť zložiek tenzora napätí závisí od orientácie sústavy súradníc. Na to aby sme získali maximálne hodnoty napätí v telese, musíme vhodne orientovať sústavu súradníc, tak aby v nej nadobúdali hodnoty napätí extrémy. Hľadáme kedy bude normálové napätie maximálne. Vychádzame z rovnice pre transformáciu σx' a použijeme matematický postup derivácie funkcie pre získanie extrému

![]()
Z úpravy vyplýva, že extrémne normálové napätie bude v rovine, v ktorej je šmykové napätie nulové. Takáto rovina sa nazýva hlavná rovina a napätie jej prislúchajúce nazývame hlavné napätie. V odvodenej rovnosti si označíme uhol pootočenia sústavy súradníc ako e, teda vzťah bude mať tvar ![]() a vyjadríme si hľadaný uhol
a vyjadríme si hľadaný uhol
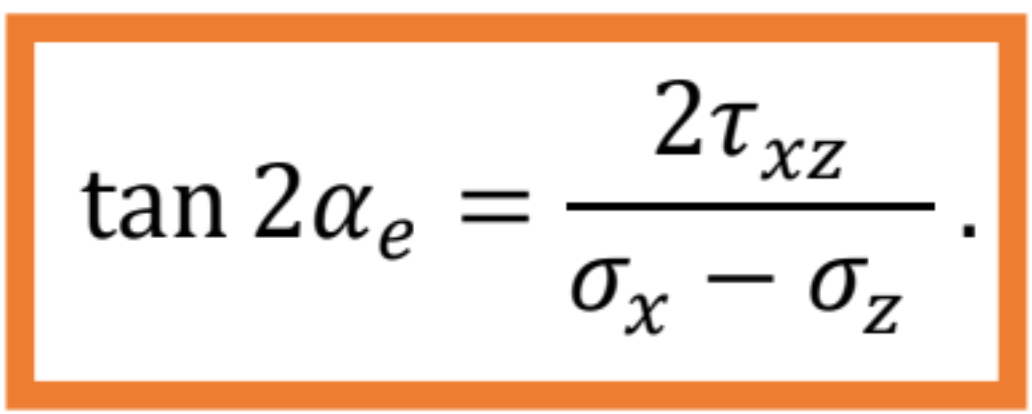
Dosadením uhla αe do transformačných vzťahov alebo do transformačnej matice T, môžeme vypočítať hodnoty hlavných napätí, čo sú maximálna a minimálna hodnota normálových napätí.
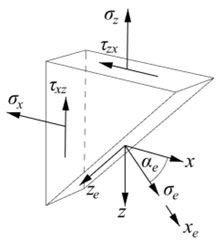
Rovnovážny diferenciálny element skosený v rovine hlavného napätia (xeze)
Aby sme odvodili vzťah pre priame vyčíslenie hlavných napätí vychádzame opäť zo skoseného diferenciálneho elementu. Skosenie definuje pootočenie sústavy súradníc o uhol αe, ktorý je teraz neznámy. Zapíšeme si rovnováhu síl vo vodorovnom a zvislom smere
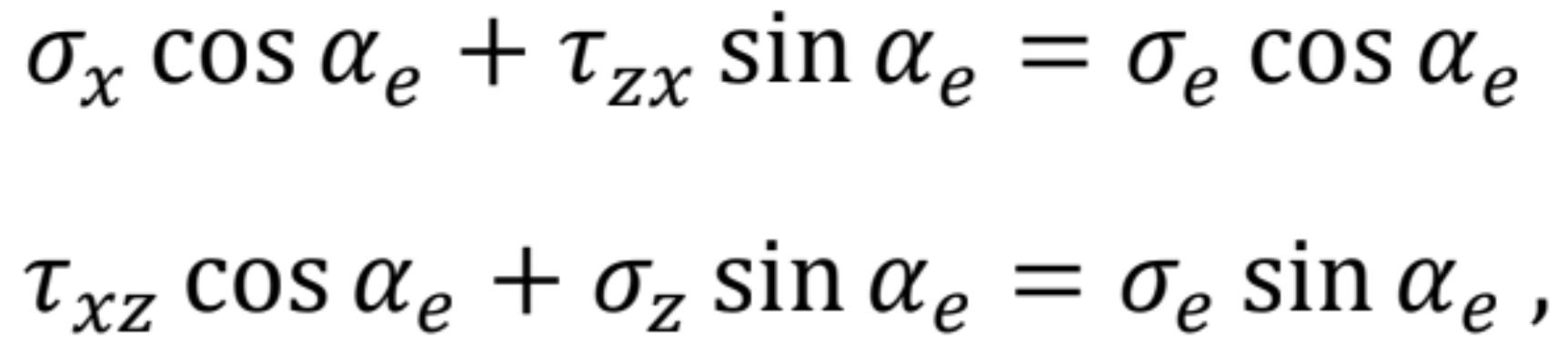
ktoré upravíme
![]()
![]()
Dostali sme homogénnu sústavu rovníc s neznámymi sinαe a cosαe. Matica koeficientov sústavy rovníc je
![]()
Homogénna sústava rovníc má netriviálne riešenie ak sa determinant matice koeficientov rovná nule, teda det A = 0 , čo vedie na kvadratickú rovnicu s neznámou σe
![]()
S koeficientmi ![]() bude diskriminant
bude diskriminant
![]()
Riešenie kvadratickej rovnice je ![]()

Hlavné napätia označujeme σ1 a σ2, pričom uplatňujeme dohodu, že σ1>σ2, teda σ1=(σxe,σze) a σ2=(σxe,σze). Pre jednoznačné určenie smerov maximálneho a minimálneho napätia je účelné vykonať transformáciu tenzora napätí podľa už uvedených vzťahov pre transformáciu zložiek tenzora napätí.
Extrémy šmykových napätí
Uvažujeme, že stav napätosti máme popísaný v sústave súradníc hlavných napätí, pootočenej od počiatočnej sústavy súradníc o uhol αe, napätiami σxe, σze a τxeze = 0. Ak z tejto polohy pootočíme sústavu súradníc o uhol δ získame pomocou transformačných vzťahov

Z rovnosti pre τxz'' je zrejmé, že extrémnu hodnotu dosiahne šmykové napätie, ak je sin 2δ =1, a teda ![]() alebo
alebo ![]() . To znamená, že extrémne šmykové napätia pôsobia v rovinách pootočených oproti hlavným rovinám o uhol 45° a (z posledného vzťahu) nadobúdajú hodnotu
. To znamená, že extrémne šmykové napätia pôsobia v rovinách pootočených oproti hlavným rovinám o uhol 45° a (z posledného vzťahu) nadobúdajú hodnotu

Zároveň pôsobia na roviny extrémnych šmykových napätí normálové napätia
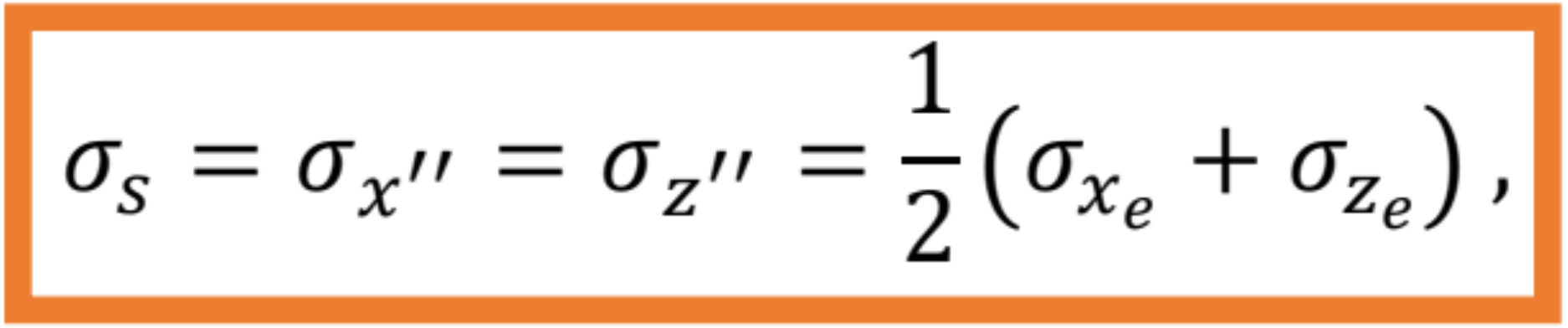
keďže ![]()
Podporené grantom: KEGA 030STU-4/2023
Vedúca projektu: Doc. Tvrdá
Zdroj: Dický, J., Mistríková, Z., Sumec, J.: Pružnosť a plasticita I. Vydavateľstvo STU. 2005.












