HISTÓRIA | Betonárske pravítko:
Tak hneď v prvopočiatkoch, v prednáškach zo železobetónu na SVŠT, sa vyhraňujú pojmy substitučný prierez, parametrické betonárske pravítko, a to všetko vo vzťahu k otázke mimostredného tlaku. Substitučný prierez totiž umožňuje pri dvakrát vystuženom priereze vytvorením pojmu totálnej výstuže postupovať ako pri jedenkrát vystuženom, ktorého neutrálna os je v tej istej polohe ako pri dvakrát vystuženom priereze.

Tabuľka je vytlačená na zadnej strane parametrického betonárskeho pravítka a jednoznačne s ním súvisí. Ono samo osebe je na svoju dobu v klasickej teórii železobetónu pozoruhodnou dimenzačnou pomôckou, ktorá v spojení s metódou substitučného prierezu dovoľovala rýchlo a ľahko, ale tiež presne dimenzovať prierezy ľubovoľného tvaru pre všetky bežné druhy namáhania.
Pravítko má svojho predchodcu v podobnom pravítku Prof. Riegra so stupnicami založenými na logaritmickom princípe. Pre namáhanie ohybom bol zvlášť dobre spracovaný rebrový a obdĺžnikový prierez, roztriedený podľa šírkových a výškových parametrov a tiež podľa veľkosti tlačenej výstuže v polohe 0,1 h. Všetky veličiny boli redukované podľa vonkajších prierezových rozmerov h/b. Uvedené Riegrovo riešenie viedlo k ťažkostiam pri excentrickom namáhaní, kde bola potrebná tiež redukcia excentricity. Riegrovo pravítko nezvládlo túto oblasť v dostatočnej šírke, pričom s ohľadom na stúpajúce percento vystuženia pri logaritmických stupniciach strácalo na presnosti odčítania. Havelkovo riešenie tieto nedostatky zásadne odstraňovalo tým, že všetky úlohy vyvodené zo spoločného teoretického základu postavilo na bázu ohybu. 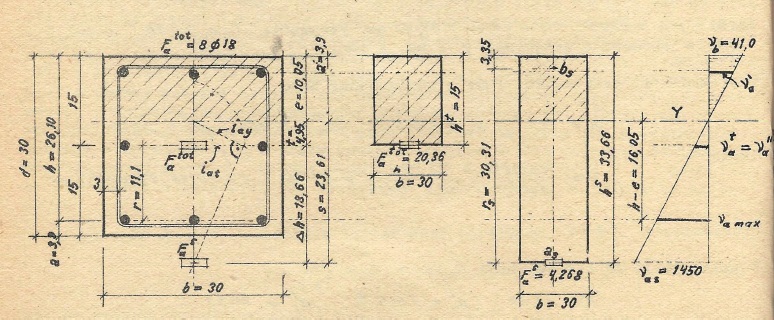 Podarilo sa to úvahou o tzv. zástupnom ohybe, ktorá je spracovaná v autorovej doktorskej práci "Mimostředný tlak prurezu ztužených s excentricitou v jedné nebo obou hlavních osách". Výsledkom tejto operácie bolo, že excentrický ťah a tlak sa mohol riešiť ako prostý ohyb. Práca na pravítku nevyhnutne priniesla so sebou ohromné množstvo vyčísľovania potrebného pre presné vynesenie funkcií a stupníc, a tým sa mladší učitelia a vedecké pomocné sily učili sústavnosti, dôkladnosti a dôslednosti. Samozrejme, že výuka prebiehala v úzkej spojitosti so spomenutými vedeckými prácami a vďaka tomu, že ich vedúci ústavu spomínal v prednáškach i skriptách, študenti sa zaujímali tiež o problematiku pravítka. V tom čase na cvičeniach sa počítalo podľa pravítka Riegrovho, keďže nové bolo iba v štádiu spracovávania.
Podarilo sa to úvahou o tzv. zástupnom ohybe, ktorá je spracovaná v autorovej doktorskej práci "Mimostředný tlak prurezu ztužených s excentricitou v jedné nebo obou hlavních osách". Výsledkom tejto operácie bolo, že excentrický ťah a tlak sa mohol riešiť ako prostý ohyb. Práca na pravítku nevyhnutne priniesla so sebou ohromné množstvo vyčísľovania potrebného pre presné vynesenie funkcií a stupníc, a tým sa mladší učitelia a vedecké pomocné sily učili sústavnosti, dôkladnosti a dôslednosti. Samozrejme, že výuka prebiehala v úzkej spojitosti so spomenutými vedeckými prácami a vďaka tomu, že ich vedúci ústavu spomínal v prednáškach i skriptách, študenti sa zaujímali tiež o problematiku pravítka. V tom čase na cvičeniach sa počítalo podľa pravítka Riegrovho, keďže nové bolo iba v štádiu spracovávania.












