Jednoduchý osový ťah alebo tlak vzniká vtedy, ak jedinou vnútornou silou v každom priereze prúta je osová sila, t. j. normálová sila prechádzajúca ťažiskom prierezu.
Výskyt osového ťahu resp. tlaku:
- priehradové sústavy,
- ťahané laná,
- centricky tlačené stĺpy,
- základové pätky.
Odvodené vzťahy v tejto kapitole majú obmedzenú platnosť a platia len pre krátke masívnejšie prúty. Problémy "štíhlych prútov", kde sa pri osovom tlaku prejaví náhodná odchýlka polohy normálovej sily od ťažiska prierezu, alebo nepatrné zakrivenie osi prúta, budú vysvetlené v kapitole "Stabilita priamych prútov".
Jednoduchým ťahom resp. tlakom sú namáhané len zvislé prúty. Pri šikmých alebo vodorovných prútoch ide o prípad osového ťahu alebo tlaku iba vtedy, ak zanedbáme vlastnú tiaž prúta.
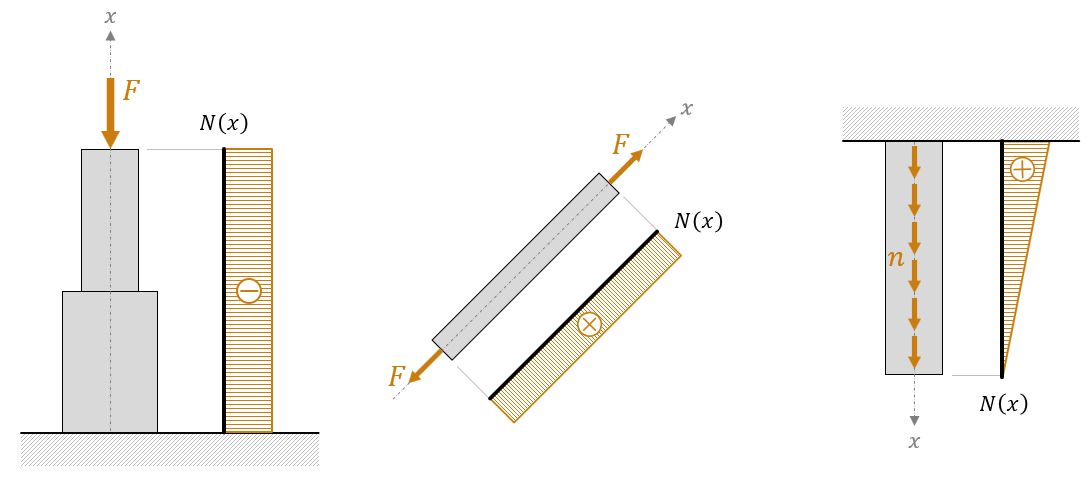
Navier a Bernoulliho hypotéza o pretvorení ťahaného resp. tlačeného prúta zavedená na základe experimentu:
- Priama os prúta pred deformáciou zostane priama aj po deformácii.
- Prierezy prúta zostanú aj po deformácii rovinné a kolmé na os prúta, pričom sa zmenia ich vzdialenosti. Pri ťahu vznikne k oddialeniu prierezov, pri tlaku k ich priblíženiu.
- Rozmery prierezov sa pri osovom ťahu zmenšujú a pri tlaku zväčšujú, pričom pomerná zmena dĺžky v priečnom smere je úmerná ku pomernej zmene dĺžky v pozdĺžnom smere prúta.
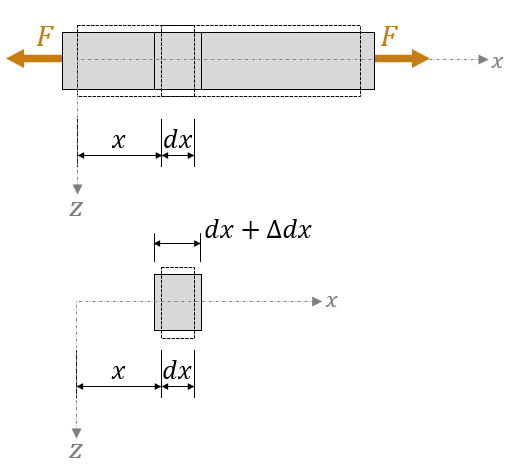
Dva nekonečne blízke rovnobežné prierezy vzdialené o dx na základe hypotézy budú opäť rovnobežné a zmenia svoju vzdialenosť o hodnotu Δdx. Preto pomerná zmena dĺžky v pozdĺžnom smere εx (t. j. pomerná zmena dĺžky v smere osi prúta x) je vo všetkých bodoch priečneho rezu konštantná.
Geometrická hypotéza pre daný prierez je:
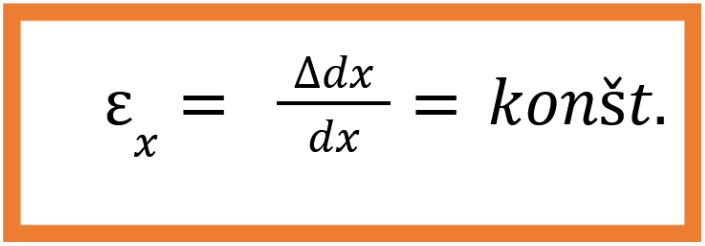
V uvedenej hypotéze je vyjadrená iba zmena v geometrii prúta namáhaného osovým ťahom resp. tlakom bez ohľadu na veľkosť zaťaženia a materiál prúta.












