Strata stability – nastáva v prípade namáhania štíhlych priamych prútov tlakom v osi prúta – prút si nezachová svoj tvar a vybočí.
Stabilita – schopnosť prvku (resp. celého systému) zachovať si tvar pri danom zaťažení.
Stabilita z mechaniky tuhých telies:
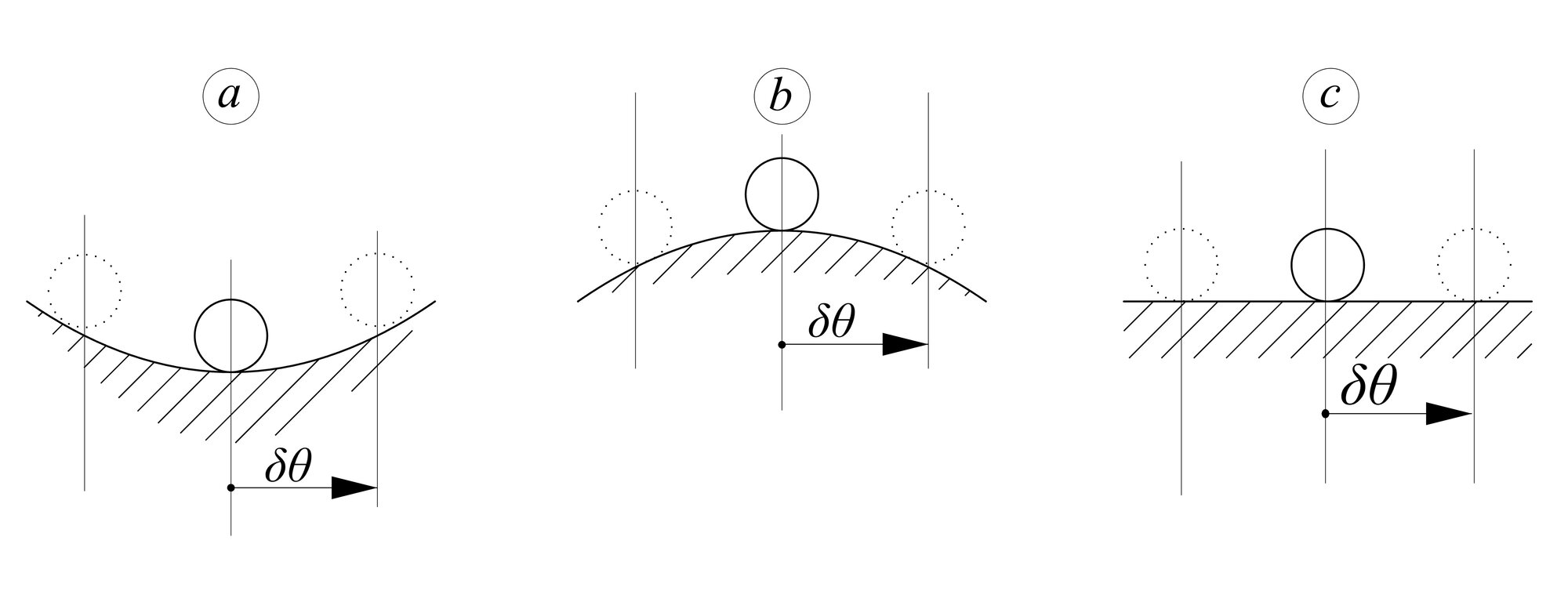
- Stabilná rovnováha – teleso sa po vychýlení vráti do východiskovej polohy. (guľôčka a)
- Nestabilná (labilná) rovnováha – stačí malý impulz a teleso sa uvedie do pohybu. Pohyb trvá dovtedy kým teleso nenadobudne novú stabilnú polohu na inom mieste. (guľôčka b)
- Indiferentná rovnováha – teleso nadobúda rovnováhu v každej blízkej vychýlenej polohe. (guľôčka c na nasledujúcom obr.)
Stabilitné kritérium pri statickej rovnováhe prúta:
- Skúmajme dokonale tuhý vertikálny prút uložený v bode a na pružine s tuhosťou k.
- Prút je zaťažený tlakovou osovou silou F a horizontálnou silou H na konci prúta (obr. a).
- Zmena odklonu prúta od vertikálnej osi (uhol θ) v závislosti od veľkosti sily F a pri veľkej a malej vodorovnej sile H je nakreslená na obr.b.
- Ak F = 0, prút môže iba rotovať okolo bodu
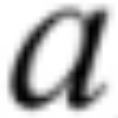. Má 1 stupeň voľnosti. - Horizontálnou silou H na konci prúta (obr. a).
- Ak prút vychýlime o veľmi malý uhol θ, klopiaci moment pri H = 0 je F.L.sin θ ≈ F.L. θ a vratný moment je k.θ.
- Stabilná rovnováha FL θ<k θ
- Nestabilná rovnováha FL θ>k θ
- Indiferentná rovnováha Fcr L θ=k θ
- Kritickú silu určíme z indiferentnej rovnováhy:
- Stabilná sústava F < Fcr
- Nestabilná sústava F > Fcr
- Indiferentná sústava F = Fcr
Bifurkačný bod C (obr.b) rozdeľuje dve vetvy rovnovážnych polôh:
- Zvislá vetva F ≤ Fcr, θ=0
- Vodorovná vetva F = Fcr, θ>0
Pri analýze rovinného vybočovania prúta budeme uvažovať dva základné modely:
- ideálny prút (Eulerovho typu) s priamou osou. Jeho vlastnosti sú idealizované (konštantný prierez, homogenita fyzikálnych vlastností, atď.).
- prút so začiatočným rovinným normovým zakrivením. Všetky imperfekcie skutočného prúta (imperfekcie od ideálneho geometrického tvaru, odchýlky v homogenite materiálu) sa vystihnú zavedením jednej maximálnej ekvivalentnej odchýlky modelu začiatočnej ohybovej čiary prúta wo = wo (x), ktorú je výhodné voliť v afinnom tvare k vlastnej funkcii, ktorá zodpovedá najmenšej hodnote kritickej sily ideálneho prúta.
Riešenie úloh teórie pružnosti:
- Teória prvého rádu – podmienky rovnováhy sa zostavovali na nedeformovanom telese.
- Teória druhého rádu – podmienky rovnováhy sa zostavovali na málo deformovanom telese.
V stabilitnej analýze ideálneho prúta sa vychádza z indiferentnej rovnováhy málo deformovaného prúta zaťaženého kritickými silami.
