Deformácia konzolovitého prúta zaťaženého silou F = Fcr uvedená na nasledujúcom obrázku.
Ohybový moment v priereze x je
![]()
Po dosadení tohto výrazu do diferenciálnej rovnice ohybovej čiary prúta dostaneme
![]()
a po úprave dostaneme
![]()
Ak
![]()
potom
![]()
Riešenie tejto diferenciálnej rovnice je funkcia
![]()
Integračné konštanty A, B a priehyb w1 určíme z troch kinematických okrajových podmienok
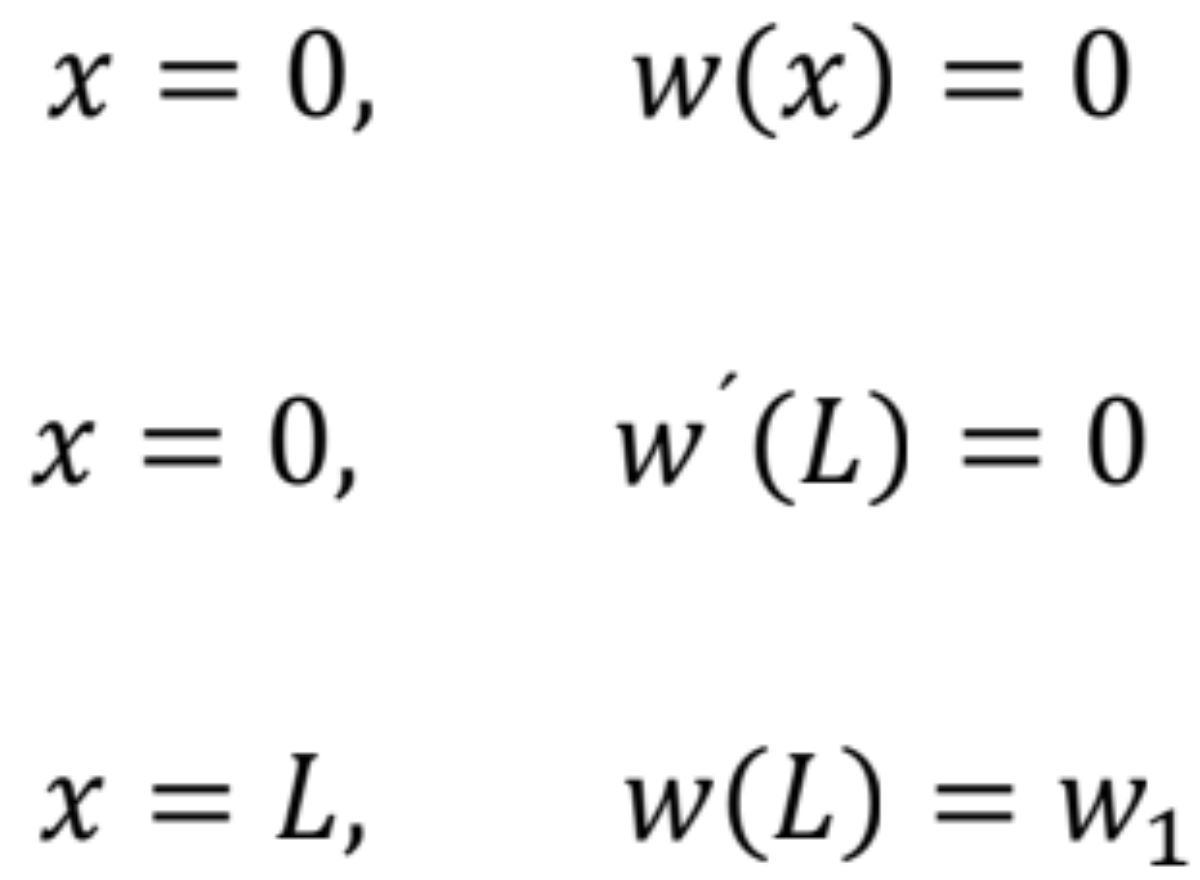
odkiaľ
![]()
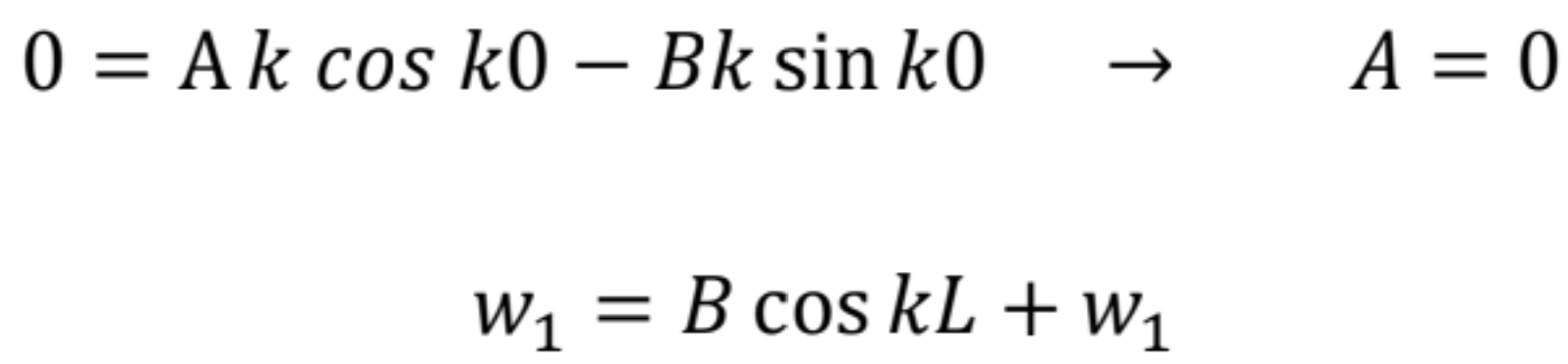
Dosadením B do poslednej z týchto rovníc a úprave dostaneme
![]()
Riešením poslednej rovnice sú korene:
![]()
Odkiaľ najmenší koreň pre n = 0 je:
![]()
a minimálne kritické zaťaženie je:
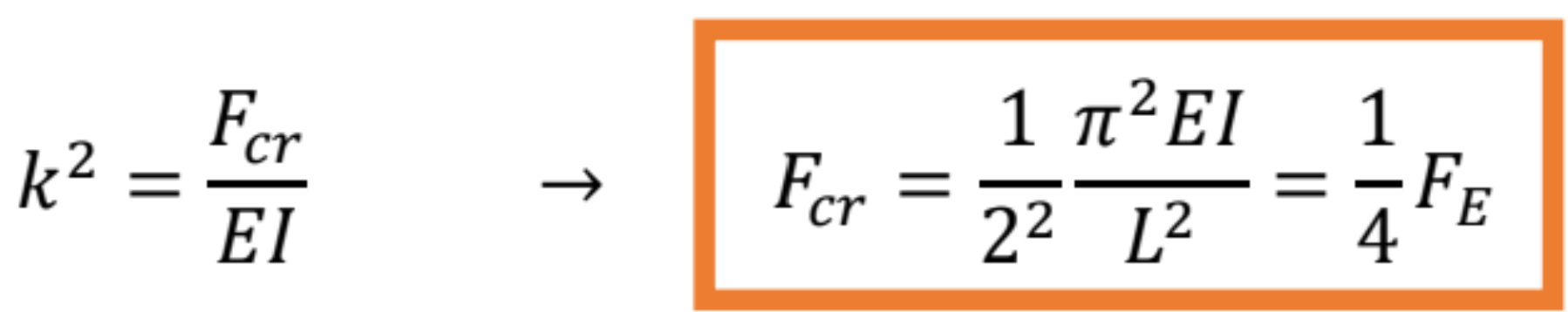
Tvar vybočenia pre konzolovitý prút bude
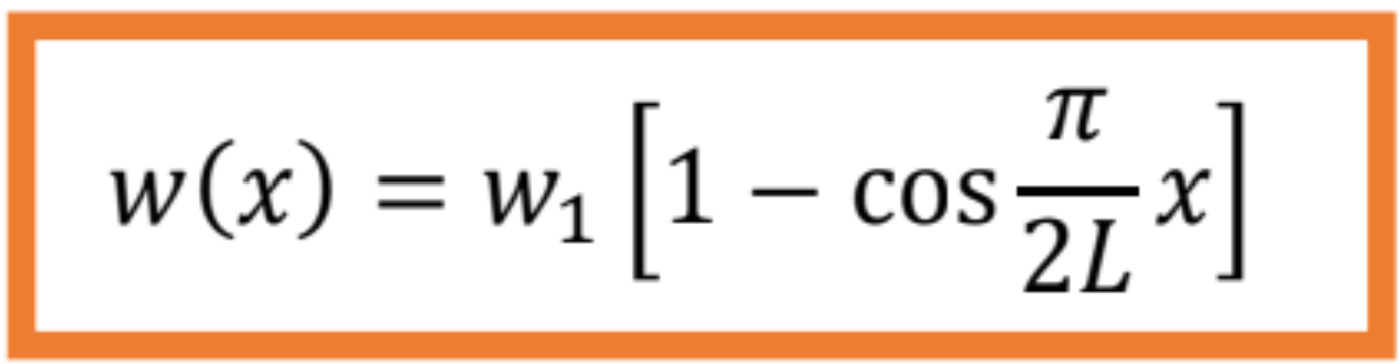
Podporené grantom: KEGA 030STU-4/2023
Vedúca projektu: Doc. Tvrdá
Zdroj: Dický, J., Mistríková, Z., Sumec, J.: Pružnosť a plasticita I. Vydavateľstvo STU. 2005.












