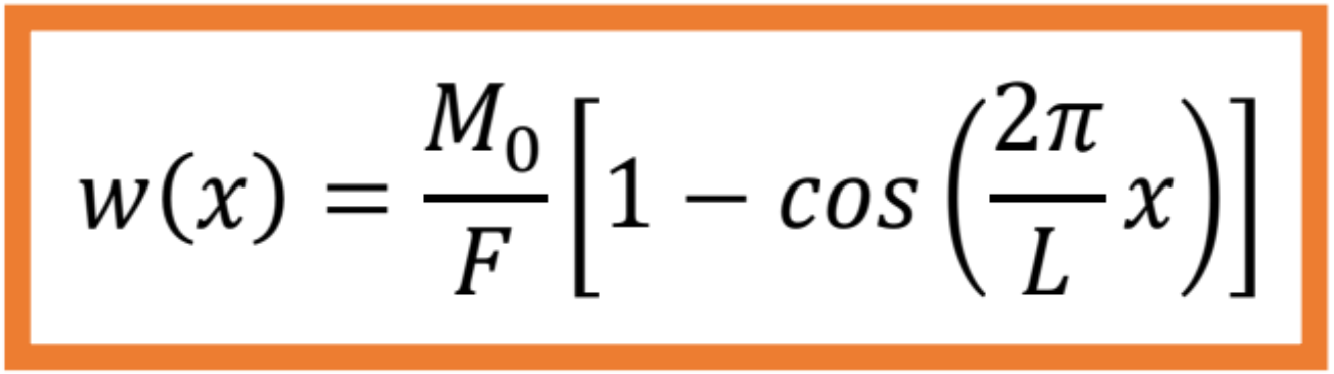Ohybový moment v priereze x je podľa obrázku je
![]()
Diferenciálna rovnica ohybovej čiary má po dosadení predchádzajúceho výrazu tvar
![]()
a po jej úprave a zavedenia konštanty k dostaneme
![]()
Riešenie diferenciálnej rovnice je v tvare funkcie:
![]()
Integračné konštanty A, B a moment M0 určíme na základe troch kinematických okrajových podmienok
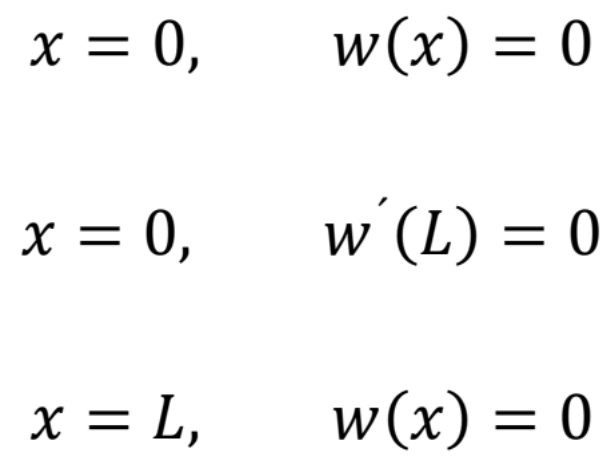
odkiaľ
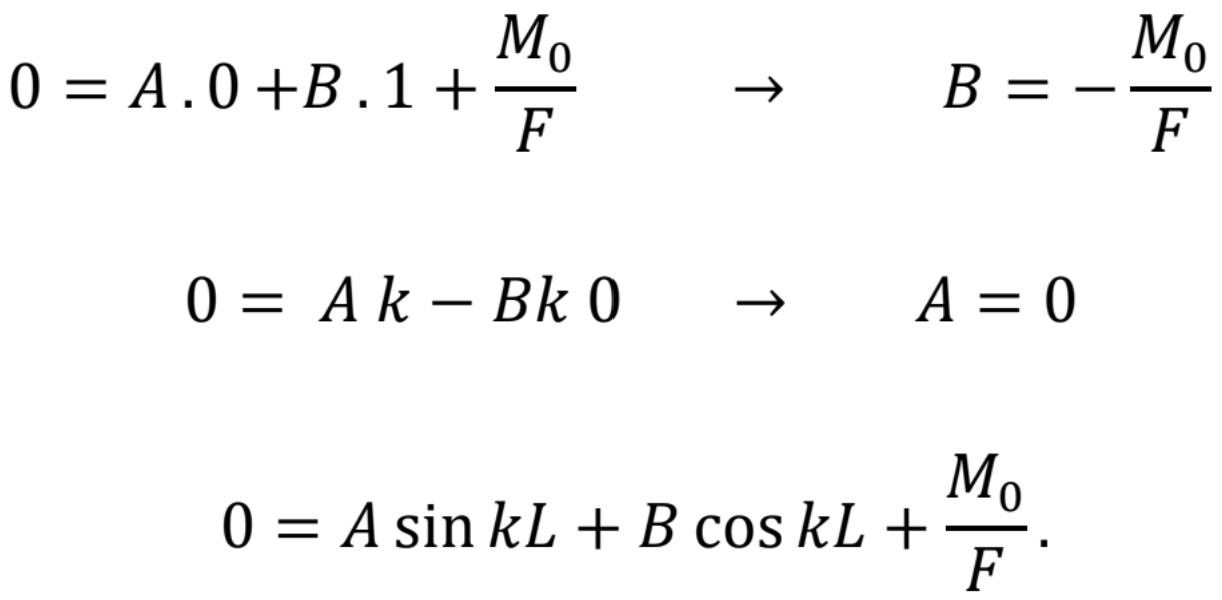
Po úprave poslednej rovnice a dosadením integračných konštánt dostaneme
![]()
Dosadením integračných rovníc do poslednej rovnice a po jej úprave dostaneme rovnicu
![]()
Minimálnu kritickú silu dostaneme pre koreň ![]() :
:
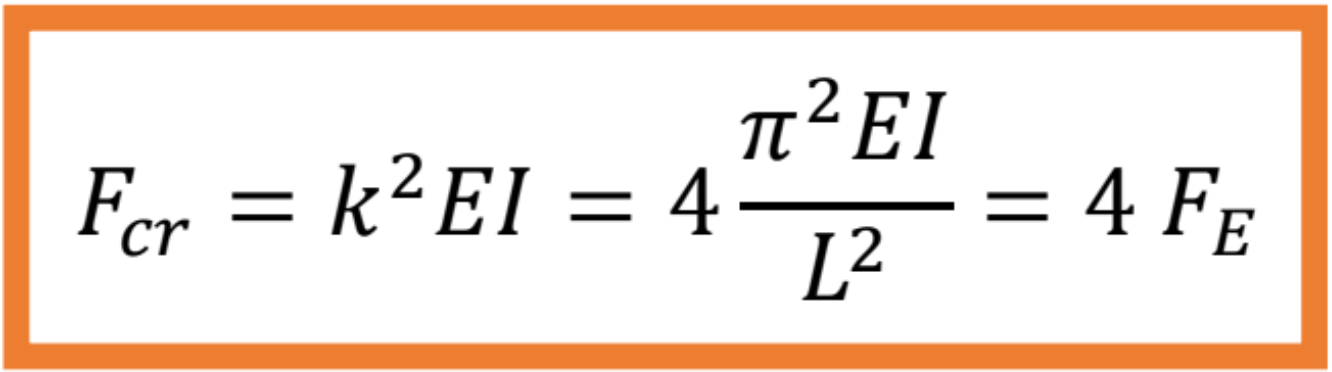
Tvar vybočenia pre prút obojstranne votknutý bude: