Skúmame prizmatický prút obojstranne kĺbovo uložený a zaťažený centricky pôsobiacou silou
![]()
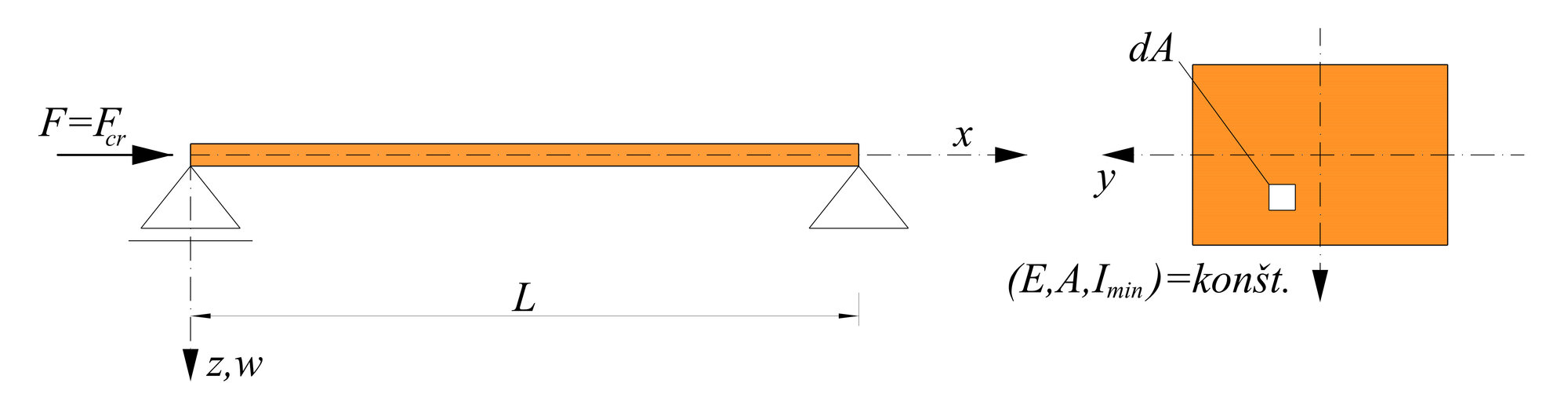
Kritická sila Fcr je sila, ktorá spôsobí vybočenie prúta kolmo na smer centrálnej hlavnej osi zotrvačnosti prierezu, ku ktorej je moment zotrvačnosti minimálny.
I = Imin .
Pre náš prípad je to os y.
Veľkosť kritickej sily určíme na zdeformovanom tvare.
Diferenciálna rovnica ohybovej čiary prúta k osi s minimálnym momentom zotrvačnosti má tvar
![]()
Z momentovej podmienky k bodu a na zdeformovanom prúte vyplýva
![]()
Dosadením tohto výrazu do diferenciálnej rovnici ohybovej čiary prúta a jeho úprave dostaneme
![]()
Kde
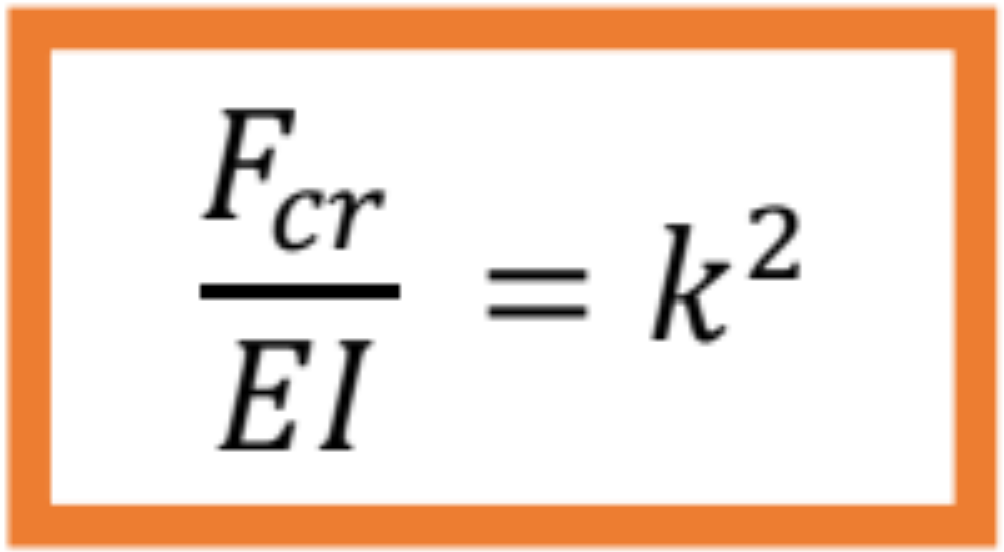
Riešenie homogénnej diferenciálnej rovnici druhého rádu s konštantnými koeficientmi je
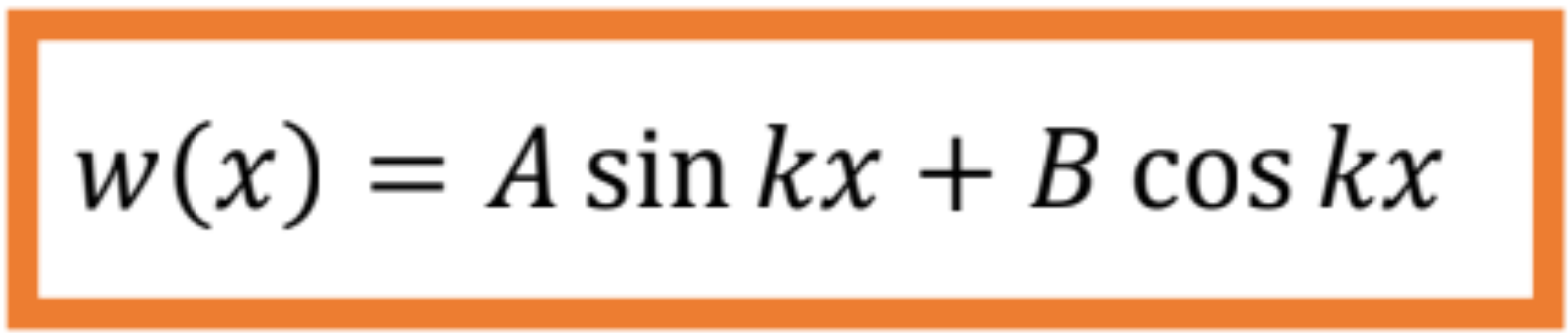
Integračné konštanty určíme z okrajových podmienok pre obojstranne kĺbovo uložený prút v okamihu straty stability:
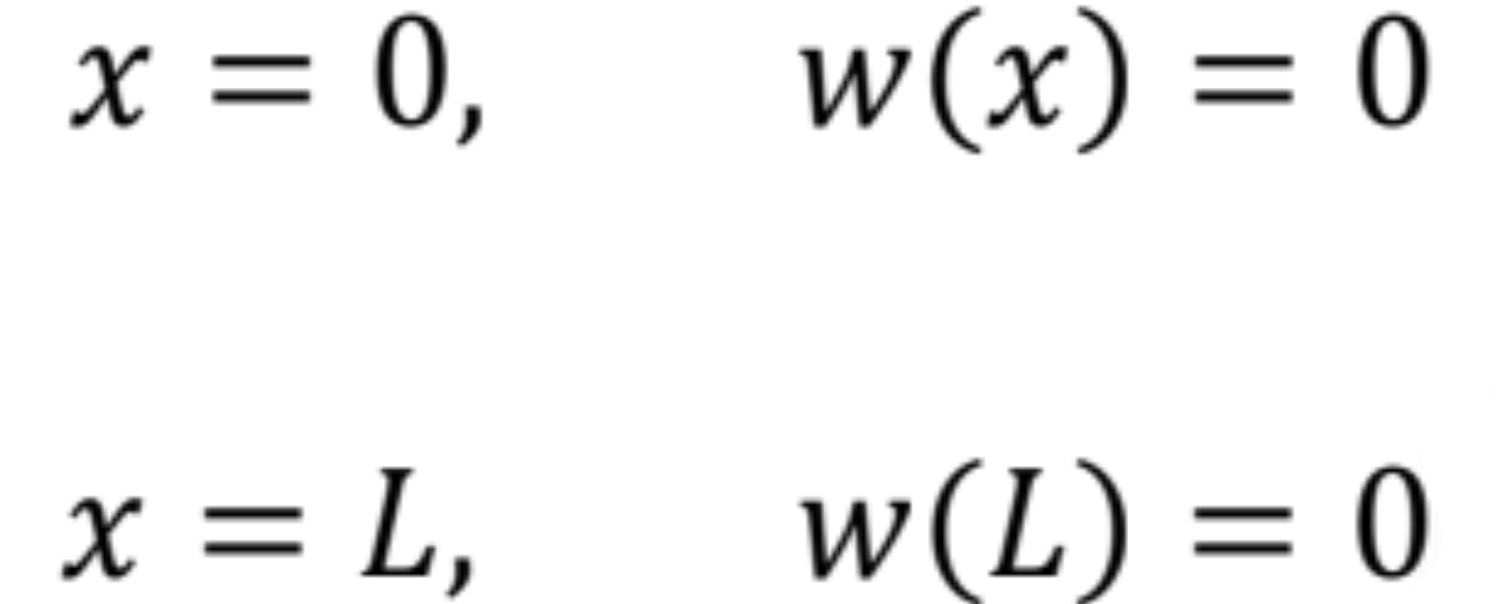
odkiaľ
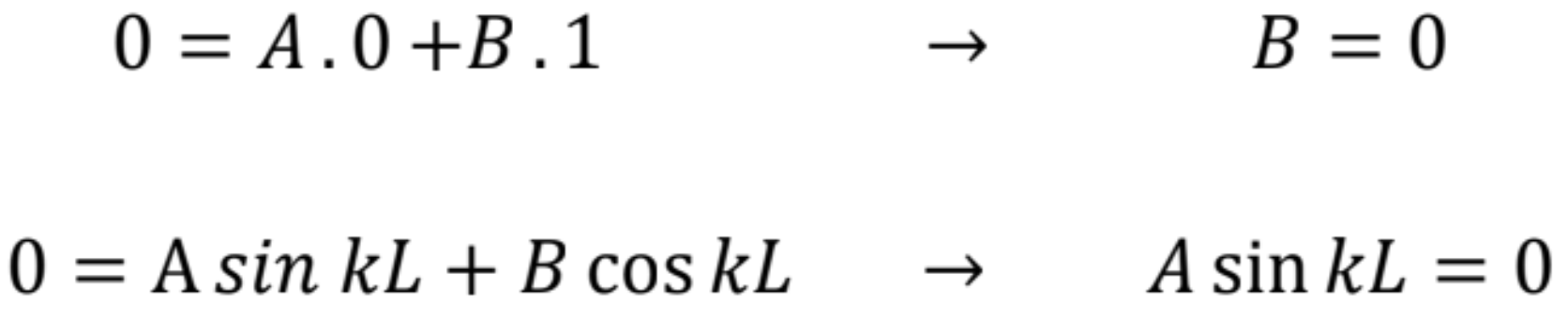
Konštanta A sa nemôže rovnať 0, pretože priehyb by bol pozdĺž prúta nulový a tak by prút nebol po strate stability. Preto pre netriviálne riešenie rovnice pre výpočet w(x) platí
![]()
Po dosadením za
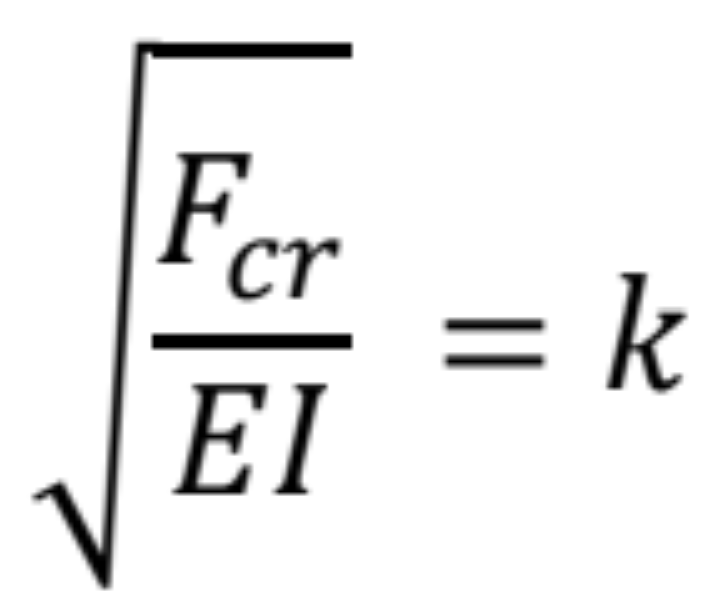
do predchádzajúcej rovnice dostaneme kritickú silu:
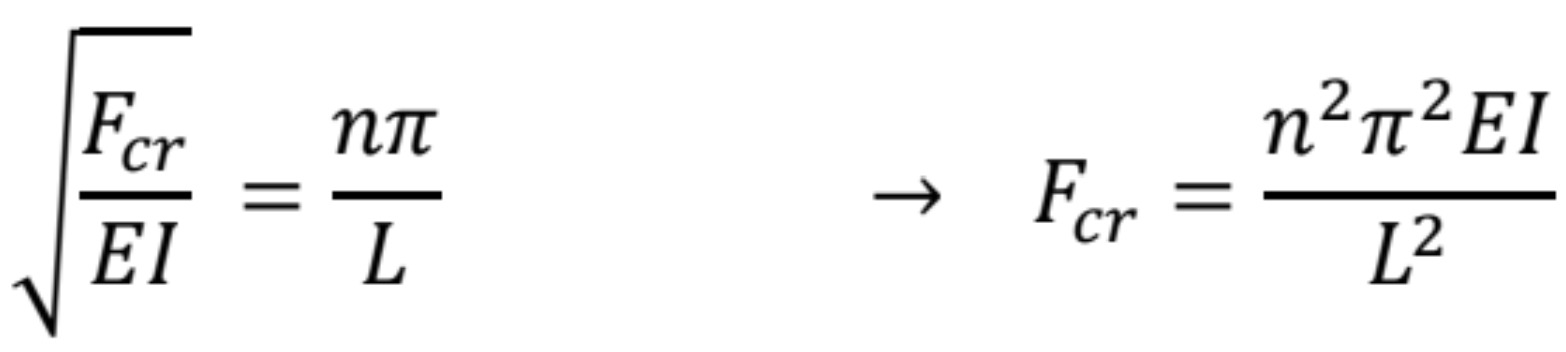
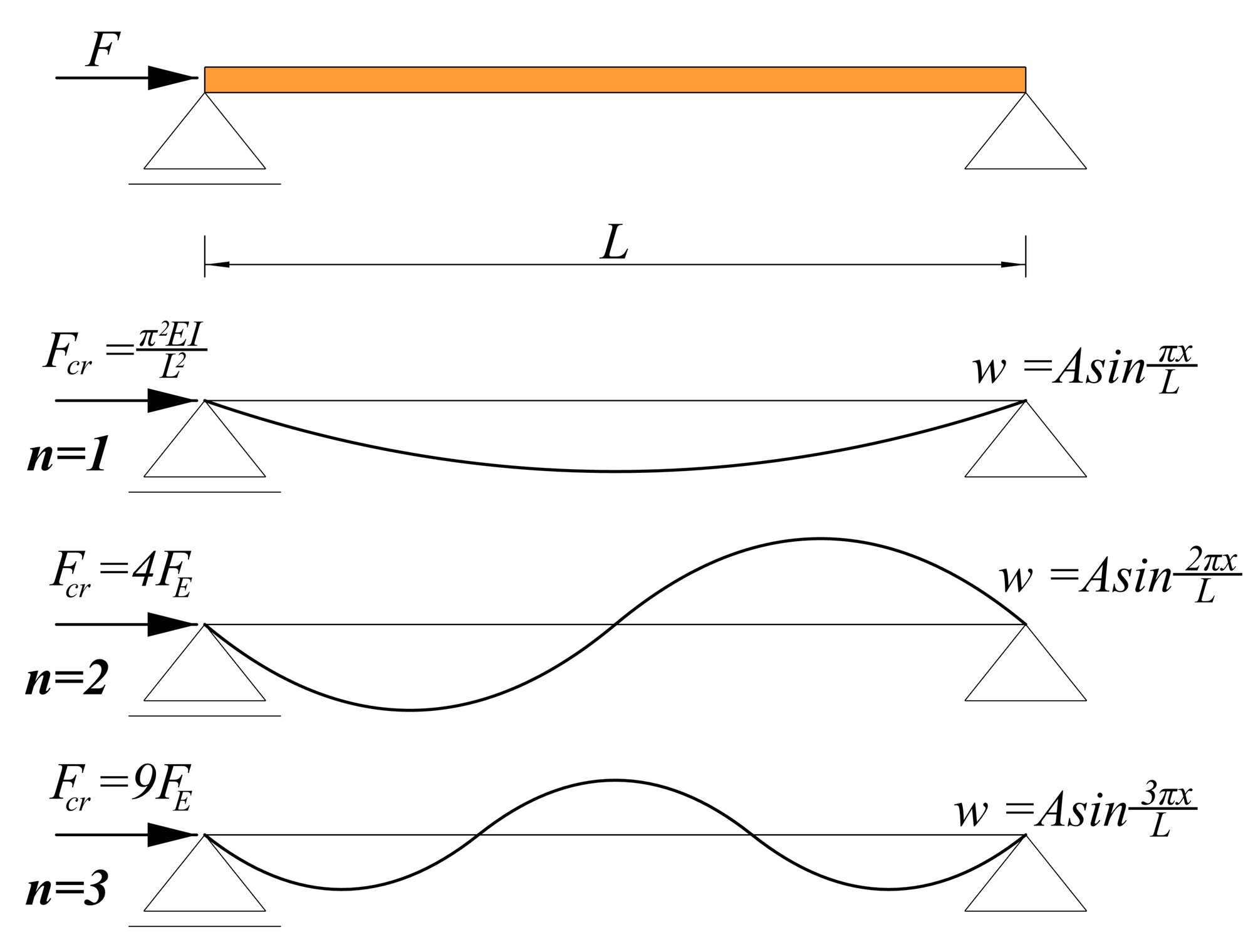
Zo všetkých hodnôt kritickej sily je pre prax zaujímavá len sila pre n = 1, ktorá zodpovedá tvaru prúta po strate stability
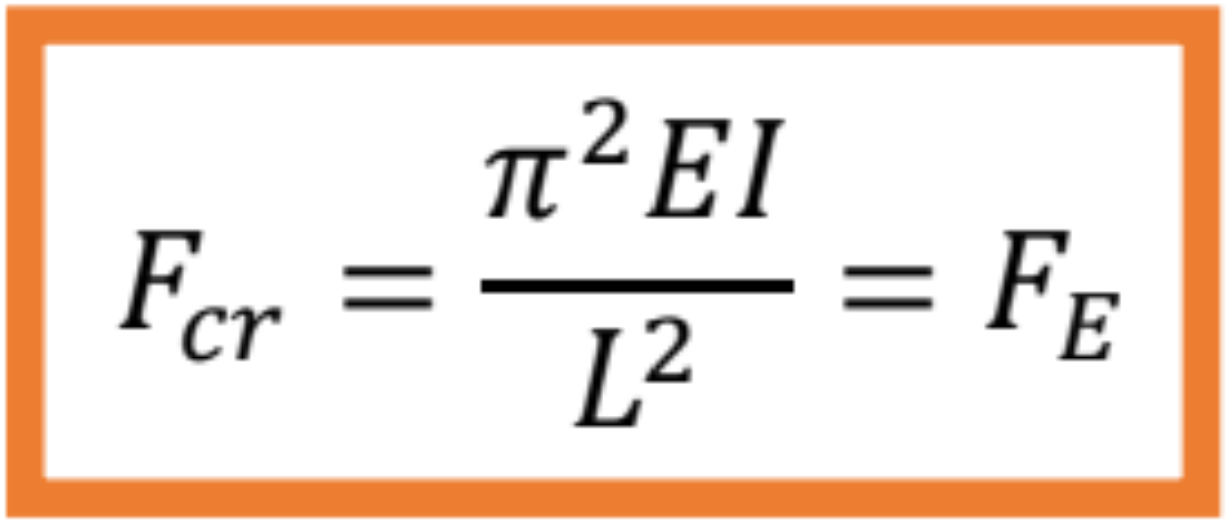
Táto sila sa nazýva Eulerová kritická sila a pre uvedený typ prúta prestavuje minimálnu kritickú silu ![]()
Tvar vybočenia pre prút obojstarnne kĺbovo uložený je po dosadení integračných konštánt v nasledujúcom tvare:
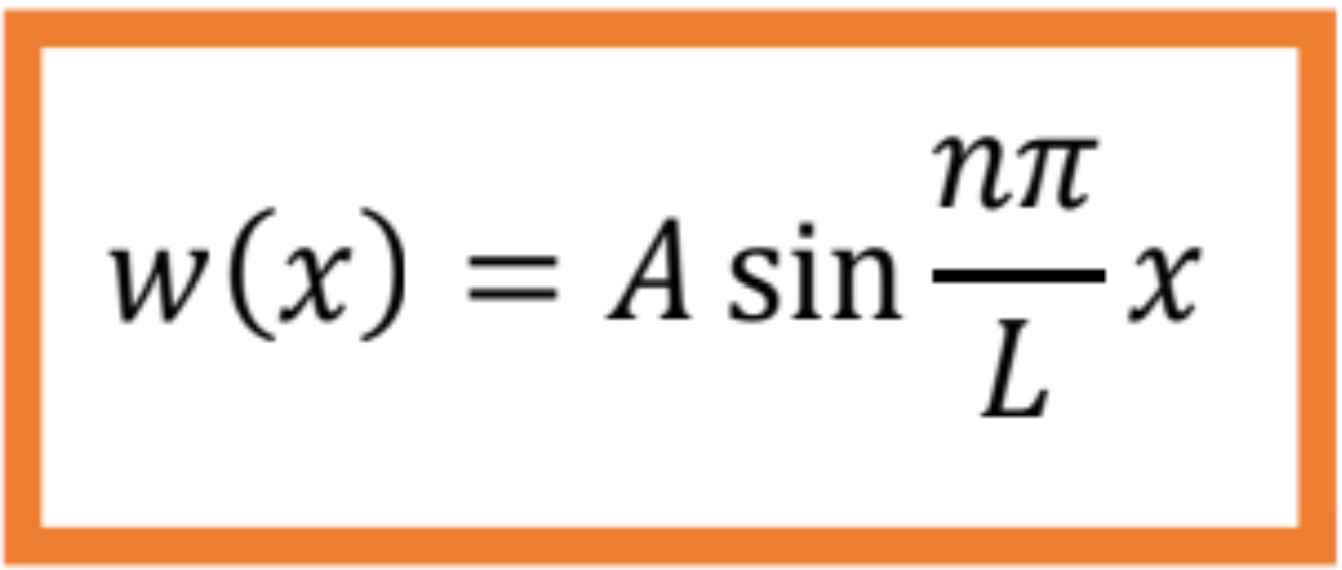
Na nasledujúcom obrázku sú uvedené prvé tri tvary vybočenia prúta po strate stability.
Podporené grantom: KEGA 030STU-4/2023
Vedúca projektu: Doc. Tvrdá
Zdroj: Dický, J., Mistríková, Z., Sumec, J.: Pružnosť a plasticita I. Vydavateľstvo STU. 2005.