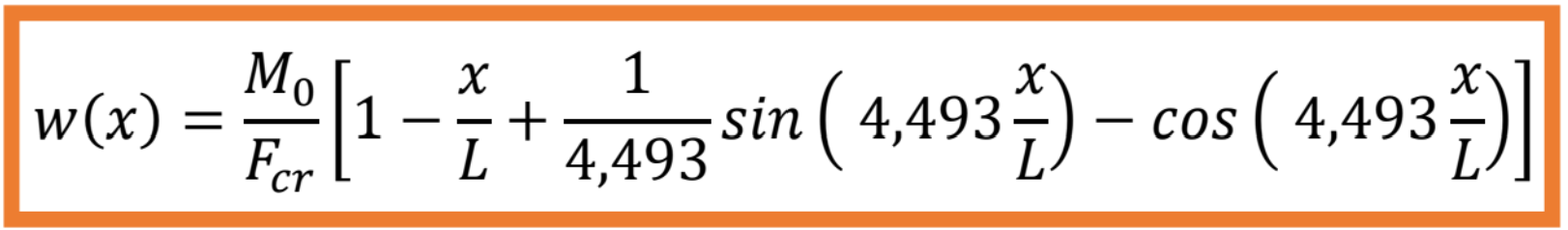Deformácia prúta na jednej strane votknutý a na druhej strane kĺbovo uložený zaťažený tlakovou silou F = Fcr môžeme vidieť na nasledujúcom obrázku.
Ohybový moment v priereze x je podľa obrázku nasledovný
![]()
a diferenciálna rovnica má tvar
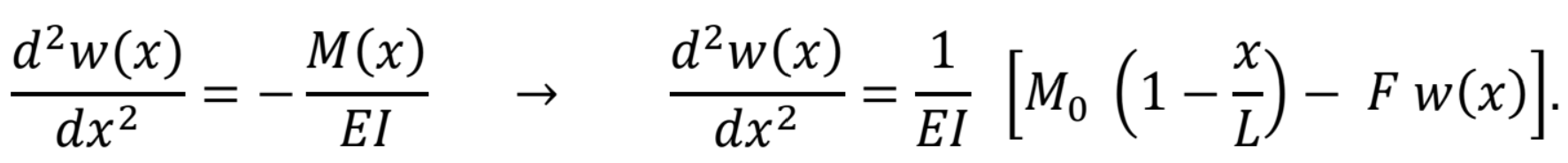
Odkiaľ
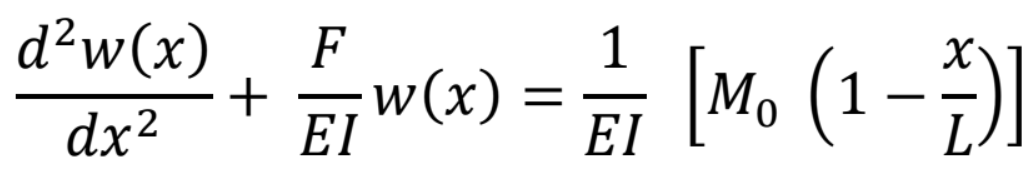
za predpokladu
![]()
a po nasledujúcej úprave dostaneme
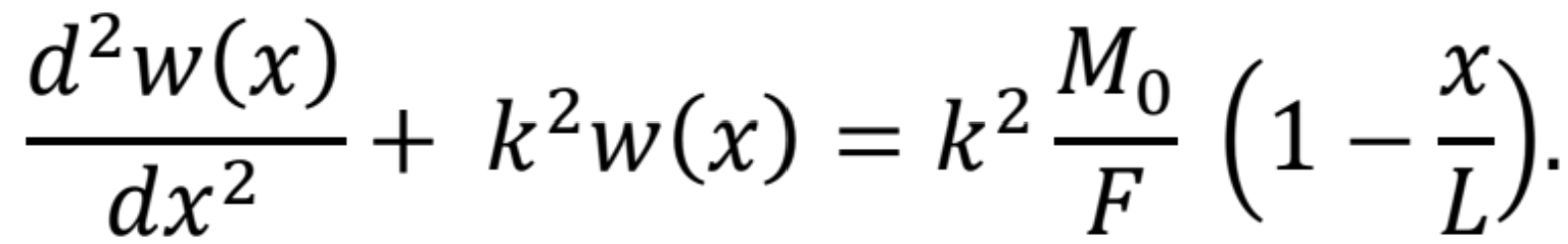
Riešenie tejto diferenciálnej rovnice je funkcia
![]()
Integračné konštanty A, B a moment M0 určíme z troch kinematických okrajových podmienok
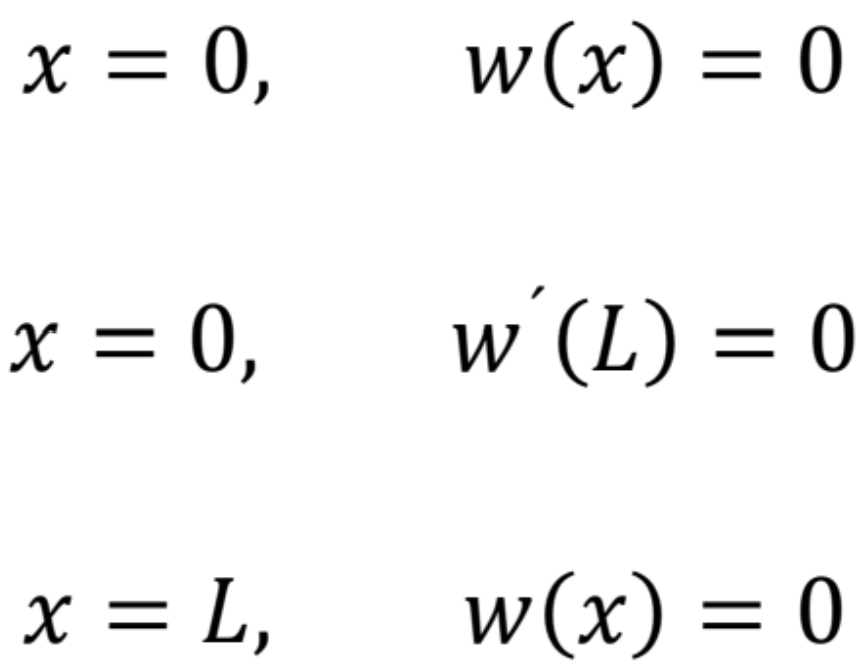
odkiaľ
![]()
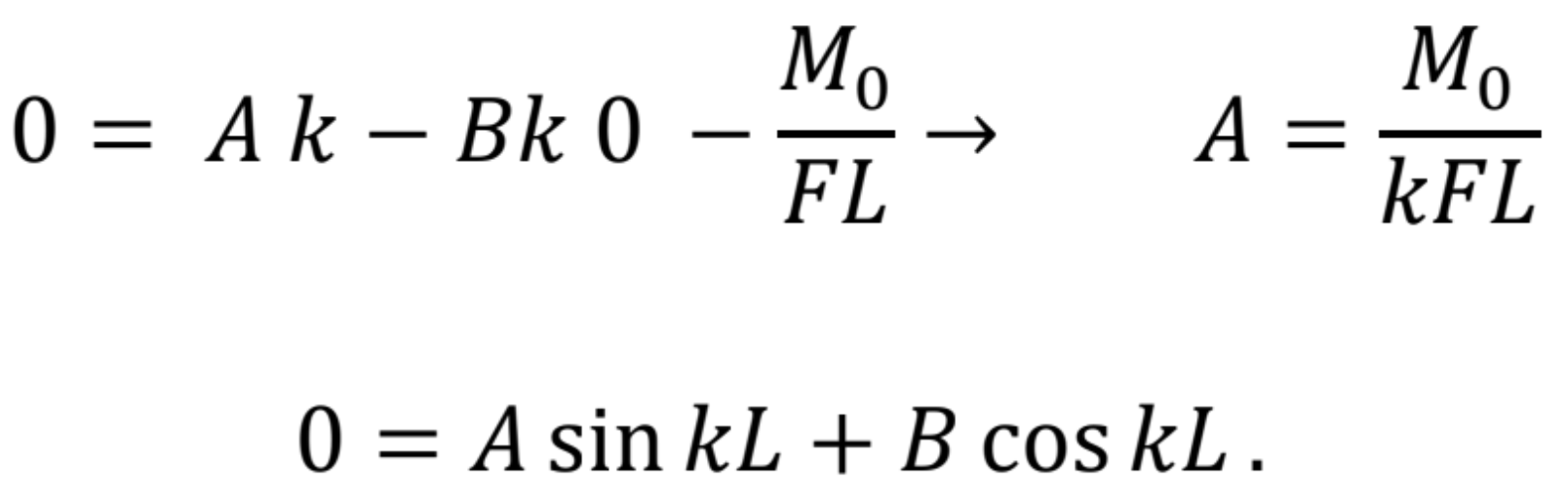
Dosadením integračných rovníc do poslednej rovnice a po jej úprave dostaneme
![]()
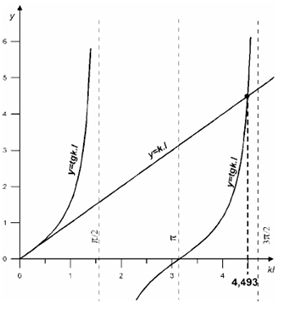
čo je transcendentná rovnica. Túto rovnicu môžeme riešiť iteračne. Korene je vidieť z grafického riešenia pre y = tg kL a y = k L. Na nasledujúcom obrázku je jej najmenší koreň
4,493=kL
A po dosadení za konštantu k
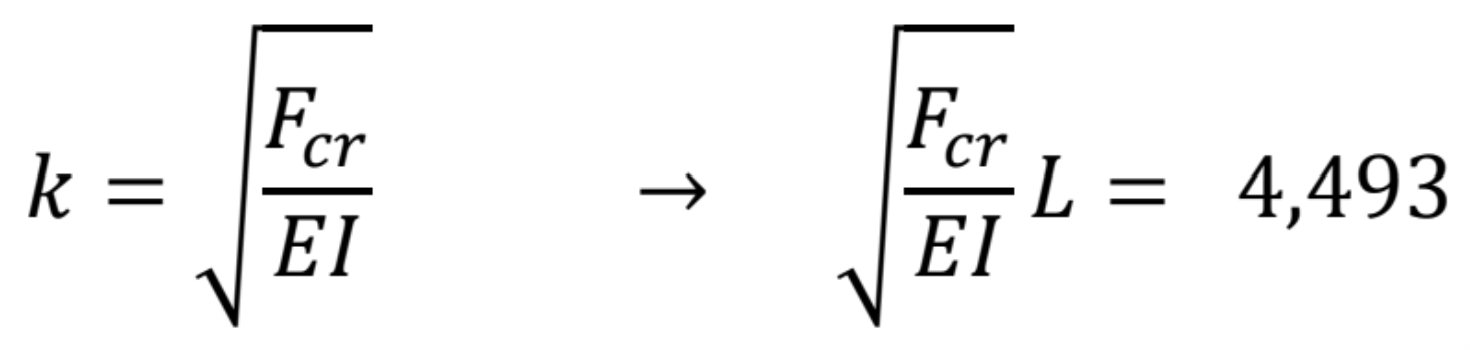
Dostávame kritické bremeno
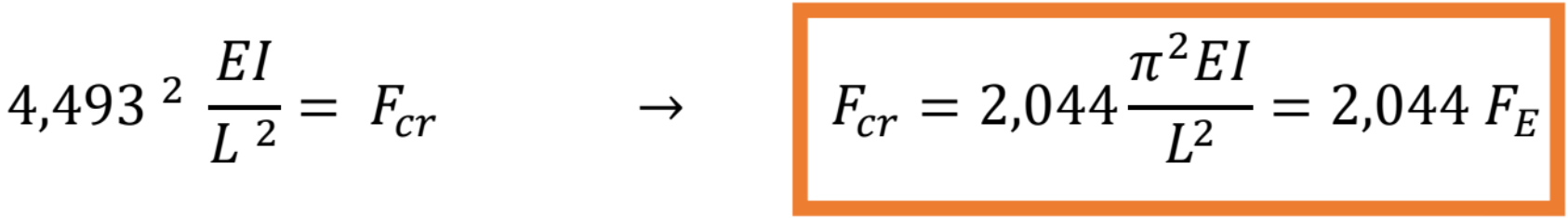
Tvar vybočenia bude