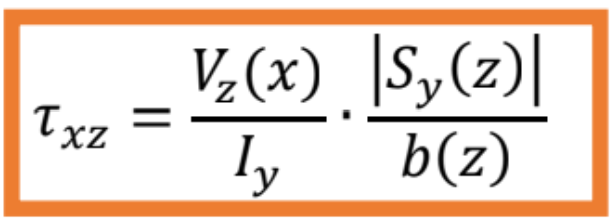Tangenciálne napätie sa vzhľadom na priečne zaťaženie mení a nie je konštantné. Teda je rozdielne v každom bode. Zároveň môžeme s istotou povedať, že šmykové napätie na voľnom povrchu stavebnej nosnej konštrukcie je nulové. V jednoduchosti sa v tejto oblasti nenachádza ďalšia nekonečne tenká plocha o ktorú by sa prvá plocha mohla trieť. Zároveň vieme skutočnosť, že najväčšia hodnota tangenciálneho napätia je v tzv. neutrálnej osi. Na tejto osi dochádza k javu, ktorý sa nazýva čistý šmyk.
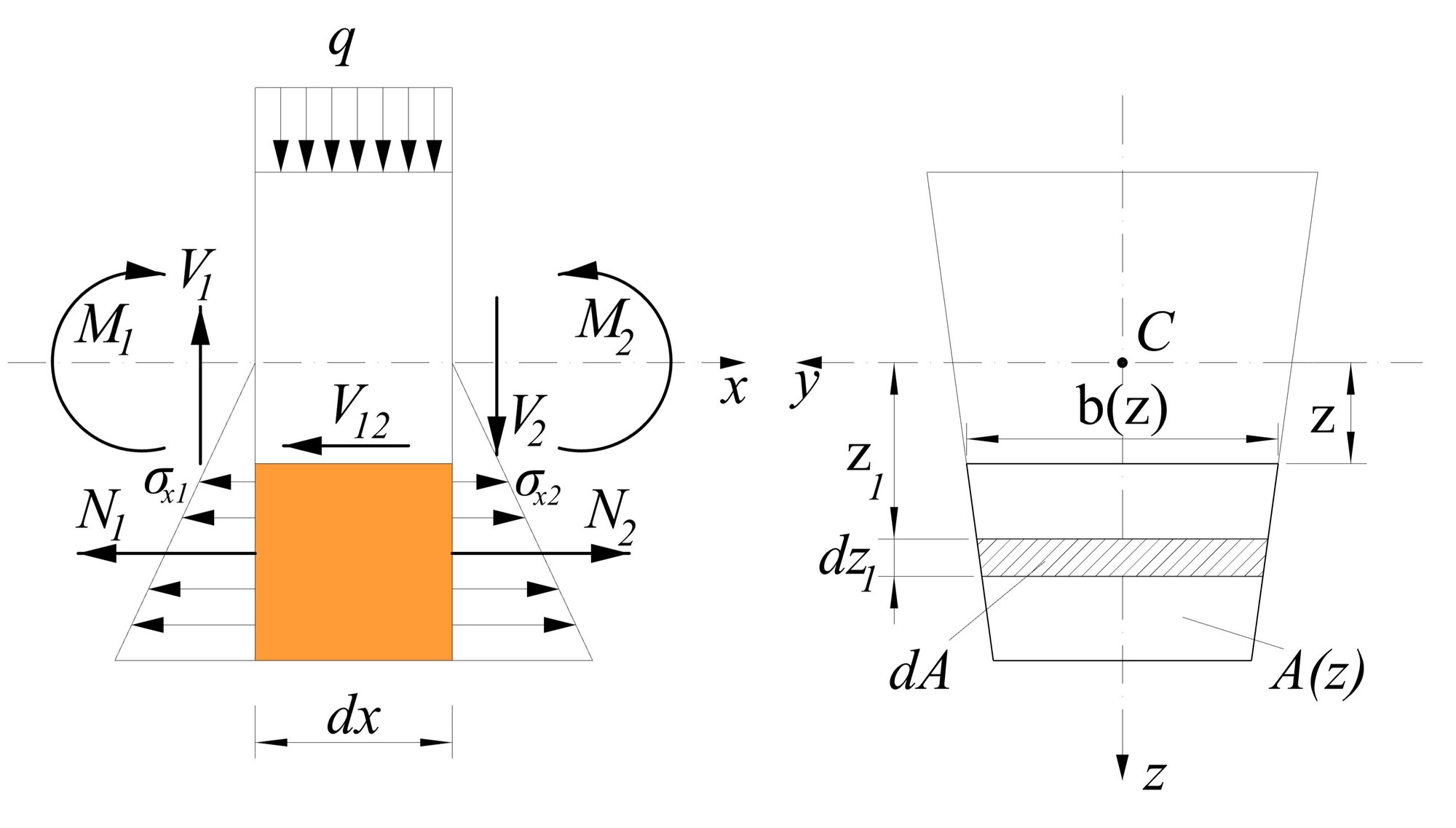
Uvažujeme nosník, ktorý zaťažený priečnym zaťažením v smere osi symetrie z tak, že v prierezoch vznikajú okrem ohybových momentov My aj priečne sily Vz.
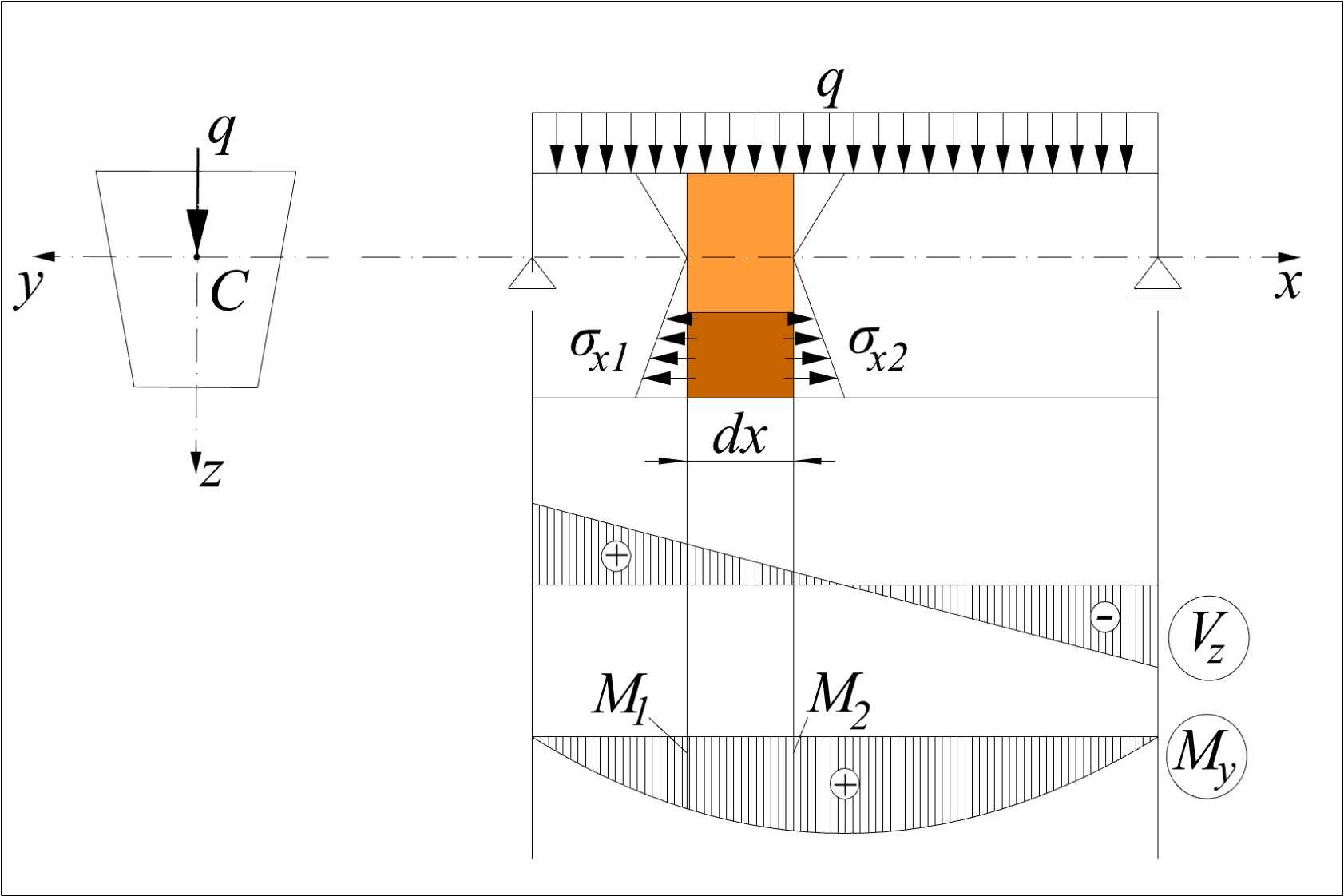
Ohybové momenty My uvedené na predchádzajúcom obrázku sa menia po dĺžke prúta. Preto aj napätia σx1 v ľavom priereze vybraného elementu a σx2 v pravom priereze elementu majú rôzne veľkosti.
Integrál normálových napätí po celom priereze, t. j. osová sila, sa však rovná nule. Statické momenty elementárnych síl k neutrálnej osi prierezu sú v rovnováhe s ohybovými momentami v prierezoch.
Iná situácia nastane, ak vybratý element z nosníka rozdelíme na dve časti, ktorý je zaťažený silami a momentami.
Normálové sily pôsobiace na element:
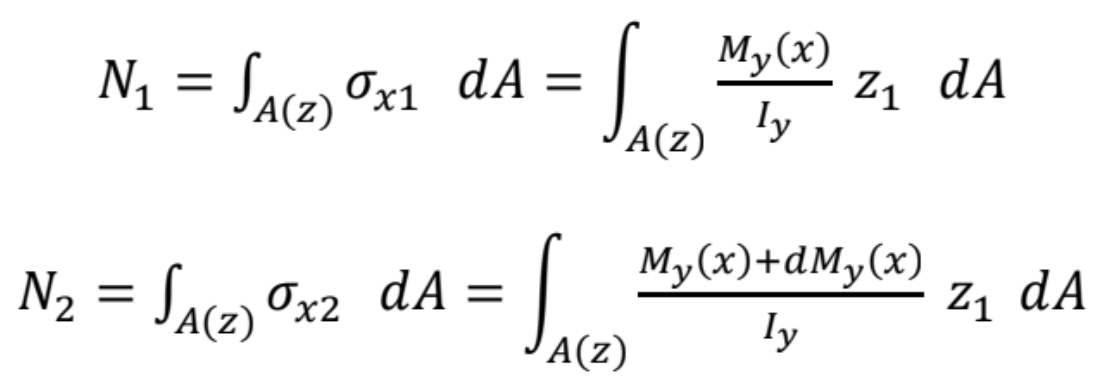
Skúmajme rovnováhu horizontálnych síl na elemente:
Po dosadení normálových síl dostaneme šmykovú silu V12
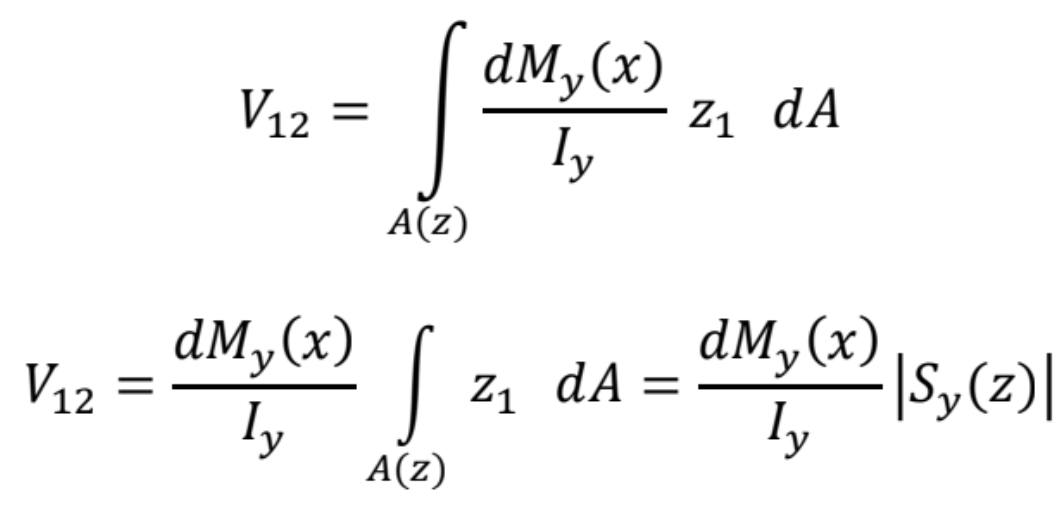
kde |Sy(z)| je absolútna hodnota statického momentu časti prierezu od hladiny z po okraj prierezu.
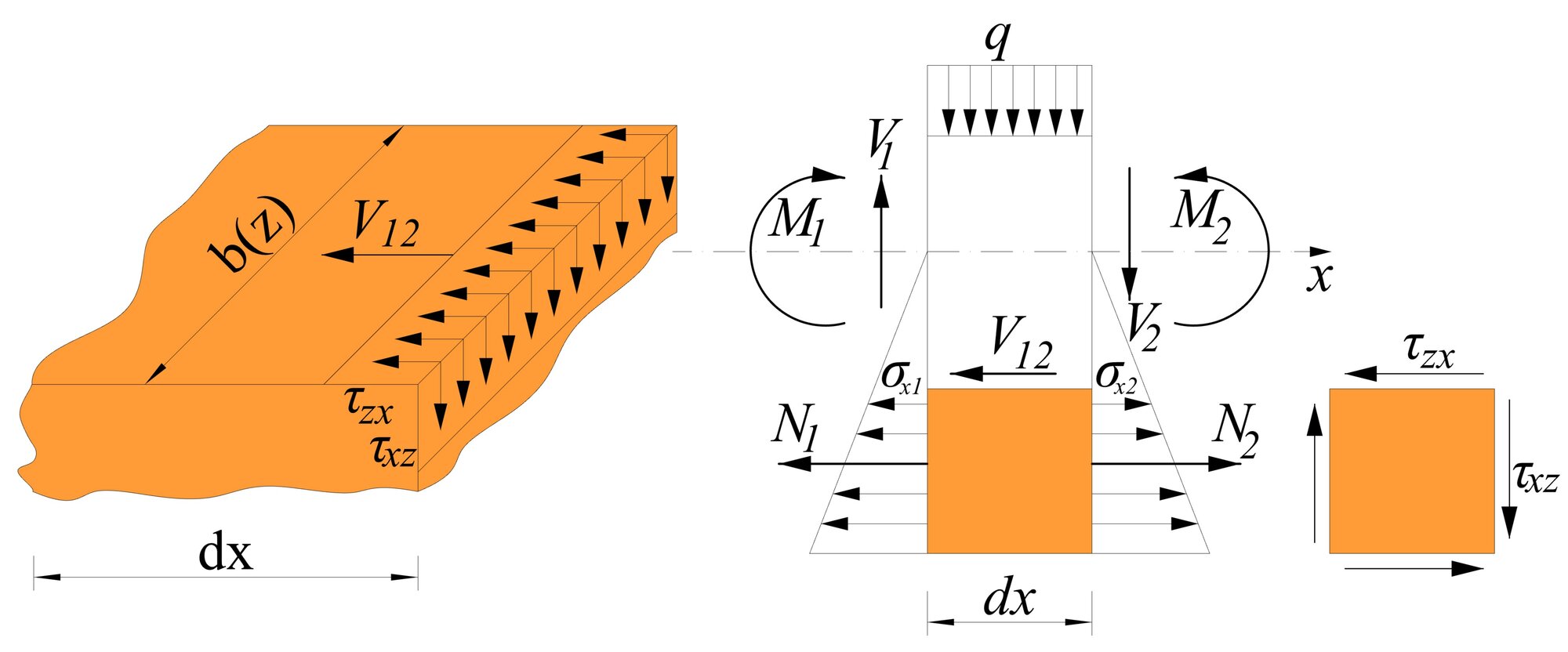
Šmyková sila V12 v priereze sa rozIoží do šmykových napätí τzx. Na ich určenie použijeme Grasshofov predpoklad pre symetrický prierez, podľa ktorého zIožka tangenciálneho napätia τzx je konštantná po šírke prierezu b(z).
Porovnaním predchádzajúcich vzťahov na výpočet šmykovej sily V12 a vyžitím vety o združenosti tangenciálnych napätiach τzx = τxz, môžeme písať
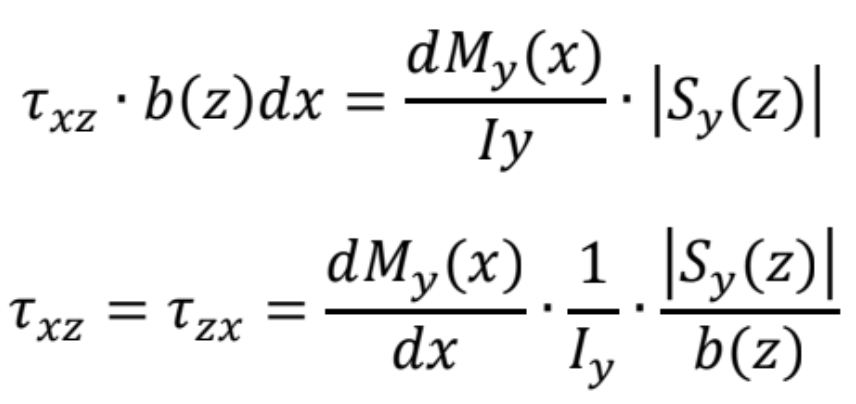
a následne využitím Schwedler-Žuravského vety 
, dostaneme vzorec na výpočet šmykového napätia v smere osi z:
